
分析 由z=x+yi(x,y∈R)满足|z|≤1,画出图形,数形结合得|z-2i|的取值范围;
由x2+y2≤1,可得2x+y-4<0,6-x-3y>0,去绝对值后得到目标函数z=-3x-4y+10,然后结合圆心到直线的距离求得|2x+y-4|+|6-x-3y|的最大值.
解答 解:∵z=x+yi(x,y∈R)满足|z|≤1,
∴在复平面内z的轨迹是以原点为圆心,以1为半径的圆及其内部,
如图,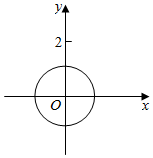
∴|z-2i|的取值范围是[1,3];
由x2+y2≤1,
可得2x+y-4<0,6-x-3y>0,
则|2x+y-4|+|6-x-3y|=-2x-y+4+6-x-3y=-3x-4y+10,
令z=-3x-4y+10,得y=-$\frac{3}{4}x$-$\frac{z}{4}+\frac{5}{2}$,
如图,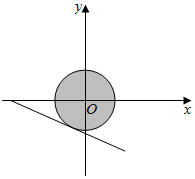
要使z=-3x-4y+10最大,则直线y=-$\frac{3}{4}x$-$\frac{z}{4}+\frac{5}{2}$在y轴上的截距最小,
由z=-3x-4y+10,得3x+4y+z-10=0.
则$\frac{|z-10|}{5}=1$,即z=15或z=5.
由题意可得z的最大值为15.
故答案为:[1,3];15.
点评 本题考查复数的代数表示法及其几何意义,考查复数模的求法,考查了简单的线性规划,考查了数形结合的解题思想方法及数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{2}}{4π}$ | B. | $\frac{4π-3\sqrt{2}}{4π}$ | C. | $\frac{1}{2π}$ | D. | $\frac{2π-1}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<-1 | B. | 0<m<1 | C. | m>1 | D. | m≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (0,1) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
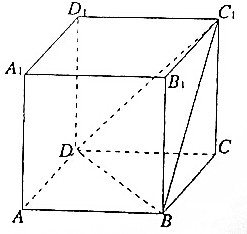 如图所示,已知棱长为1的正方体ABCD-A1B1C1D1,
如图所示,已知棱长为1的正方体ABCD-A1B1C1D1,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com