
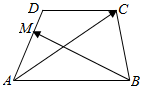
 如图,在梯形ABCD中,AB∥CD,AB=4,AD=3,CD=2,$\overrightarrow{AM}$=2$\overrightarrow{MD}$,若$\overrightarrow{AC}$•$\overrightarrow{BM}$=-3,则$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\frac{3}{2}$.
如图,在梯形ABCD中,AB∥CD,AB=4,AD=3,CD=2,$\overrightarrow{AM}$=2$\overrightarrow{MD}$,若$\overrightarrow{AC}$•$\overrightarrow{BM}$=-3,则$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\frac{3}{2}$. 分析 设∠DAB=θ,根据$\overrightarrow{AC}$•$\overrightarrow{BM}$=($\overrightarrow{AD}$-$\overrightarrow{CD}$)($\overrightarrow{AM}$-$\overrightarrow{AB}$)=($\overrightarrow{AD}$-$\overrightarrow{CD}$)($\frac{2}{3}$$\overrightarrow{AD}$-$\overrightarrow{AB}$)=3,化简计算求出cosθ=$\frac{1}{8}$,再根据向量数量积公式计算即可.
解答 解:设∠DAB=θ,
∵AB∥CD,
∴∠D=180°-θ
∵$\overrightarrow{AM}$=2$\overrightarrow{MD}$,
∴$\overrightarrow{AC}$•$\overrightarrow{BM}$=($\overrightarrow{AD}$-$\overrightarrow{CD}$)($\overrightarrow{AM}$-$\overrightarrow{AB}$),
=($\overrightarrow{AD}$-$\overrightarrow{CD}$)($\frac{2}{3}$$\overrightarrow{AD}$-$\overrightarrow{AB}$),
=$\frac{2}{3}$|$\overrightarrow{AD}$|2-$\overrightarrow{AD}$•$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{CD}$•$\overrightarrow{AD}$+$\overrightarrow{CD}$•$\overrightarrow{AB}$,
=$\frac{2}{3}$|$\overrightarrow{AD}$|2-|$\overrightarrow{AD}$|•|$\overrightarrow{AB}$|cosθ-$\frac{2}{3}$|$\overrightarrow{CD}$|•|$\overrightarrow{AD}$|cos(180°-θ)+|$\overrightarrow{CD}$|•|$\overrightarrow{AB}$|cos180°,
=$\frac{2}{3}$×32-3×4cosθ+$\frac{2}{3}×$2×3cosθ-2×4
=-2-8cosθ=-3,
∴cosθ=$\frac{1}{8}$,
∴$\overrightarrow{AD}$•$\overrightarrow{AB}$=|$\overrightarrow{AD}$|•|$\overrightarrow{AB}$|cosθ=3×4×$\frac{1}{8}$=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$
点评 本题考查了向量的数量积运算和向量的加减的几何意义,属于中档题.


科目:高中数学 来源: 题型:解答题
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [235,240) | 24 | 0.24 |
| 第二组 | [240,245) | 16 | ② |
| 第三组 | [245,250) | ① | 0.3 |
| 第四组 | [250,255) | 20 | 0.20 |
| 第五组 | [255,260] | 10 | 0.10 |
| 合 计 | 100 | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\sqrt{2}$ | B. | $\frac{1}{2}$+$\sqrt{2}$ | C. | 1+$\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}+\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{4}{3}$,$\frac{4}{3}$] | B. | [-$\frac{4}{3}$,0] | C. | [0,$\frac{4}{3}$] | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com