
分析 (1)设x∈(0,-e],则-x∈[-e,0),故f(-x)=-ax-ln(x),根据函数的奇偶性求出此时的解析式,即可得到函数在定义域内的解析式;
(2)假设存在实数a满足条件,通过讨论a的范围,利用函数的单调性求出函数的最小值,解出a的值即可.
解答 解:(1)当x∈(0,e]时,-x∈[-e,0),
则f(-x)=a(-x)-lnx,
又f(x)是奇函数,故f(x)=-f(-x)=ax+lnx,
故f(x)=$\left\{\begin{array}{l}{ax-ln(-x),-e≤x<0}\\{ax+lnx,0<x≤e}\end{array}\right.$;
(2)当x∈(0,e]时,f(x)=ax+lnx,
f′(x)=a+$\frac{1}{x}$=$\frac{ax+1}{x}$,
①当a≥0时,f′(x)>0,f(x)在区间(0,e]递增,
故函数f(x)在区间(0,e]上的最大值是f(e)=ae+1=2,
故a=$\frac{1}{e}$>0满足题意;
②当-$\frac{1}{a}$≥e,即-$\frac{1}{e}$≤a<0时,f′(x)=a+$\frac{1}{x}$≥-$\frac{1}{e}$+$\frac{1}{x}$≥-$\frac{1}{e}$+$\frac{1}{e}$=0,
故f(x)在(0,e]递增,
此时f(x)在区间(0,e]的最大值是f(e)=ae+1=2,
则a=$\frac{1}{e}$>0,不满足条件=$\frac{1}{e}$≤a<0;
③当a<-$\frac{1}{e}$时,可得f(x)在区间(0,-$\frac{1}{a}$]递增,在区间[-$\frac{1}{a}$,e]递减,
故x=-$\frac{1}{a}$时,f(x)max=f(-$\frac{1}{a}$)=-1+ln(-$\frac{1}{a}$),
令f(-$\frac{1}{a}$)=2,得a=-$\frac{1}{{e}^{3}}$>0$\frac{1}{e}$,不满足条件,
综上a=$\frac{1}{e}$时,函数f(x)在区间(0,e]上的最大值是2.
点评 本题考查对数函数的单调性和特殊点,函数的奇偶性,利用导数研究函数得最值,体现了分类讨论的数学思想,确定函数的最小值,是解题的难点和关键.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{3}{2}$,$\frac{2}{3}$] | B. | [-6,2] | C. | [-1,$\frac{7}{2}$] | D. | [-4,$\frac{2}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:解答题
已知椭圆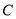 :
: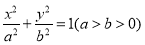 的左焦点为
的左焦点为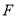 ,
, 为椭圆上一点,
为椭圆上一点,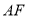 交
交 轴于点
轴于点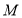 ,且
,且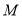 为
为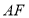 的中点.
的中点.
(1)求椭圆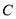 的方程;
的方程;
(2)直线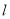 与椭圆
与椭圆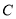 有且只有一个公共点
有且只有一个公共点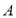 ,平行于
,平行于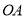 的直线交
的直线交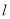 于
于 ,交椭圆
,交椭圆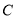 于不同的亮点
于不同的亮点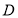 ,
,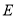 ,问是否存在常熟
,问是否存在常熟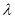 ,使得
,使得 ,若存在,求出
,若存在,求出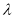 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$] | C. | [1,$\sqrt{2}$] | D. | [$\frac{2\sqrt{3}}{3}$,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:解答题
在一个盒子里装有6张卡片,上面分别写着如下定义域为 的函数:
的函数:
 ,
,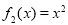 ,
,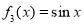 ,
,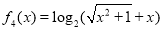 ,
, ,
,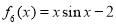 .
.
(1)现在从盒子中任意取两张卡片,记事件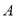 为“这两张卡片上函数相加,所得新函数是奇函数”,求事件
为“这两张卡片上函数相加,所得新函数是奇函数”,求事件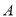 的概率;
的概率;
(2)从盒中不放回逐一抽取卡片,若取到一张卡片上的函数是偶函数则停止抽取,否则继续进行,记停止时抽取次数为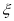 ,写出
,写出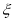 的分布列,并求其数学期望
的分布列,并求其数学期望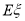 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com