
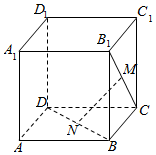
 如图,在正方体ABCD-A1B1C1D1中,点N,M分别是BD,B1C的点.
如图,在正方体ABCD-A1B1C1D1中,点N,M分别是BD,B1C的点.分析 (1)连接AC,AB1,利用三角形的中位线定理证明MN∥AB1,即可证明MN∥平面ABB1A1;
(2)结论仍成立,过点M作MP∥B1B,交BC于点P,连接NP,证明平面MNP∥平面ABB1A1,即可证明MN∥平面ABB1A1..
解答 证明:(1)如图1,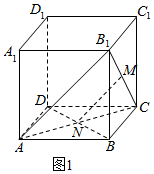
连接AC,AB1,
∵ABCD是正方形,N是BD中点,
∴N是AC中点,
又∵M是CB1中点,
∴MN∥AB1,
∵MN?平面ABB1A1,AB1?平面ABB1A1,
∴MN∥平面ABB1A1;
(2)结论仍成立,证明如下;
如图2,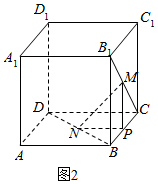
过点M作MP∥B1B,交BC于点P,连接NP,
∵MP∥B1B,∴$\frac{{B}_{1}M}{MC}$=$\frac{BP}{PC}$,
又$\frac{{B}_{1}M}{MC}$=$\frac{BN}{ND}$=$\frac{1}{2}$,∴$\frac{BN}{ND}$=$\frac{BP}{PC}$,∴NP∥DC,
又AB∥CD,∴NP∥AB;
由MP∥B1B,MP?平面ABB1A1,B1B?平面ABB1A1,∴MP∥平面ABB1A1,
同理,NP∥平面ABB1A1,
又MP?平面MNP,MP?平面MNP,
∴平面MNP∥平面ABB1A1,
又MN?平面MNP,
∴MN∥平面ABB1A1.
点评 本题考查了线线平行、线面平行和面面平行的判定与性质定理的应用问题,是中档题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$或-$\frac{1}{2}$ | B. | 1 | C. | 1或-1 | D. | 2或-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P((A1+A2)|$\overline{B}$)=P(A1|$\overline{B}$)+P(A2|$\overline{B}$) | B. | P(A1B+A2B)=P(A1B)+P(A2B) | ||
| C. | P(A1+A2)=P(A1|B)+P(A2|B) | D. | P(B)=P(A1)P(B|A1)+P(A2)P(B|A2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
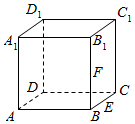
| A. | 直线AA1 | B. | 直线A1B1 | C. | 直线A1D1 | D. | 直线B1C1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com