
分析 根据题意$\left\{\begin{array}{l}{2l{nx}_{1}{{-x}_{1}}^{2}-{mx}_{1}=0①}\\{2l{nx}_{2}{{-x}_{2}}^{2}-{mx}_{2}=0②}\end{array}\right.$,作差得2ln$\frac{{x}_{2}}{{x}_{1}}$-(x2-x1)(x2+x1)-m(x2-x1)=0,整理式子,向题意靠拢;利用导数g′(x)与中点坐标公式,利用换元法得出函数g(t)其中t=$\frac{{x}_{2}}{{x}_{1}}$>1,判断g(t)的单调性,即可得出结论g'(x0)≠0.
解答 解:根据题意,得$\left\{\begin{array}{l}{2l{nx}_{1}{{-x}_{1}}^{2}-{mx}_{1}=0①}\\{2l{nx}_{2}{{-x}_{2}}^{2}-{mx}_{2}=0②}\end{array}\right.$;
②-①得,2ln$\frac{{x}_{2}}{{x}_{1}}$-(x2-x1)(x2+x1)-m(x2-x1)=0,
∴2ln$\frac{{x}_{2}}{{x}_{1}}$=(x2-x1)(x2+x1+m);(整理式子,向题意靠拢)
假设g′(x0)=0,
即g′(x0)=$\frac{-{{2x}_{0}}^{2}-{mx}_{0}+2}{{x}_{0}}$=$\frac{4}{{x}_{1}{+x}_{2}}$-(x1+x2)-m=0,(中点坐标公式2x0=x1+x2)
∴x1+x2+m=$\frac{4}{{x}_{1}{+x}_{2}}$,
上下同除以x,另t=$\frac{{x}_{2}}{{x}_{1}}$>1,
∴lnt=$\frac{2(t-1)}{t+1}$(t>1);
令g(t)=lnt-$\frac{2t-2}{t+1}$,
在g′(t)=$\frac{{(t-1)}^{2}}{{t(t+1)}^{2}}$>0,
∴g(t)>g(1)=0,
∴lnt≠$\frac{2(t-1)}{t+1}$,
即g'(x0)≠0.
点评 本题考查了函数的单调性质与导数的综合应用问题,也考查了转化思想的应用问题,是难题.


科目:高中数学 来源: 题型:选择题
| A. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α⊥平面β,过α内任意一点作交线的垂线,那么此垂线必垂直于β | |
| D. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| x/万户 | 1 | 1.1 | 1.5 | 1.6 | 1.8 |
| y/万立方米 | 6 | 7 | 9 | 11 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{5}$ | B. | 0 | C. | -$\frac{4}{5}$ | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
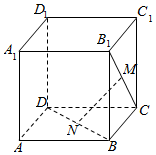 如图,在正方体ABCD-A1B1C1D1中,点N,M分别是BD,B1C的点.
如图,在正方体ABCD-A1B1C1D1中,点N,M分别是BD,B1C的点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com