Question

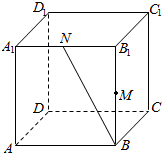
4．棱长为1的正方体ABCD-A₁B₁C₁D₁中，M，N分别是A₁B₁，BB₁的中点，点P在正方体的表面上运动，则总能使MP⊥BN的点P所形成图形的周长是（　　）

• A． 4
• B． $2+\sqrt{2}$
• C． $3+\sqrt{5}$
• D． $2+\sqrt{5}$

Answer 1

分析 取CC₁的中点G，连接DGMA，设BN交AM与点E，则使BN与MP垂直的点P所构成的轨迹为矩形ADGM，由此可得使BN与MP垂直的点P所构成的轨迹的周长．

解答 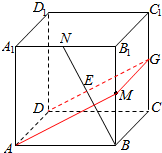解：如图，取CC₁的中点G，连接DGMA，设BN交AM与点E，则MG∥BC，
∵BC⊥平面ABA₁B₁，NB?平面ABA₁B₁，
∴NB⊥MG，
∵正方体的棱长为1，M，N分别是A₁B₁，BB₁的中点，
△BEM中，∠MBE=30°，∠BME=60°
∴∠MEB=90°，即BN⊥AM，MG∩AM=M，
∴NB⊥平面ADGM，
∴使NB与MP垂直的点P所构成的轨迹为矩形ADGM，
∵正方体的棱长为1
∴故由勾股定理可得，使B₁C与MP垂直的点P所构成的轨迹的周长等于2+$\sqrt{5}$．
故选：D．

点评 本题主要考查了立体几何中的轨迹问题，考查学生的分析解决问题的能力，解题的关键是确定使BN与MP垂直的点P所构成的轨迹，属于中档题．