
分析 (1)由f(x)=log2(x+1)的定义域为集合A,求出A的集合,由集合B={x|ax-1<0,a∈N*},求出B的集合,然后再由指数函数的性质求出集合C.
(2)由集合A,集合B求出A∩B,再由C?(A∩B),即可得到a的值.
解答 解:由函数f(x)=log2(x+1)的定义域为集合A,得A=(-1,+∞),集合B={x|ax-1<0,a∈N*}={x|$x<\frac{1}{a}$},
(1)集合C={y|y=$(\frac{1}{2})^{x+2}}$,x∈A},$y={({\frac{1}{2}})^{x+2}}$在(-1,+∞)上单调递减,则$y∈({0,\frac{1}{2}})$,则 C=$({0,\frac{1}{2}})$;
(2)由于a∈N*,B=$({-∞,\frac{1}{a}})$,
则$A∩B=({-1,\frac{1}{a}})$,由C?(A∩B),得$\frac{1}{a}≥\frac{1}{2}$⇒a≤2.
即a=1或2.
点评 本题考查了交、并、补集的混合运算,考查了集合的包含关系判断及应用,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5\sqrt{26}}{26}$ | B. | 45 | C. | 3$\sqrt{2}$ | D. | $\frac{45}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
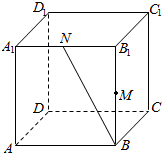 棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是A1B1,BB1的中点,点P在正方体的表面上运动,则总能使MP⊥BN的点P所形成图形的周长是( )
棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是A1B1,BB1的中点,点P在正方体的表面上运动,则总能使MP⊥BN的点P所形成图形的周长是( )| A. | 4 | B. | $2+\sqrt{2}$ | C. | $3+\sqrt{5}$ | D. | $2+\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com