
分析 (I)利用等比数列的通项公式即可得出;
(II)利用等比数列的通项公式及其前n项和公式即可得出.
解答 解:(I)∵2(an+an+2)=5an+1,n∈N*,∴$2{a}_{n}(1+{q}^{2})$=5anq,
化为2(1+q2)=5q,又q>1,
解得q=2.
(II)a52=a10,$({a}_{1}×{2}^{4})^{2}$=a1×29,解得a1=2.
∴an=2n.
∴$\frac{{a}_{n}}{{3}^{n}}$=$(\frac{2}{3})^{n}$.
∴数列{$\frac{{a}_{n}}{{3}^{n}}$}的前n项和Sn=$\frac{\frac{2}{3}[1-(\frac{2}{3})^{n}]}{1-\frac{2}{3}}$=$2[1-(\frac{2}{3})^{n}]$.
点评 本题考查了等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
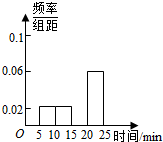 某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:
某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:| 分组 | 频数 | 频率 | |
| 一组 | 0≤t<5 | 0 | 0 |
| 二组 | 5≤t<10 | 10 | 0.10 |
| 三组 | 10≤t<15 | 10 | 0.10 |
| 四组 | 15≤t<20 | 50 | 0.50 |
| 五组 | 20≤t<25 | 30 | 0.30 |
| 合计 | 100 | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m∥β,则α∥β | B. | 若m⊥α,m⊥n,则n∥α | C. | 若m∥α,m∥n,则n∥α | D. | 若m⊥α,m∥β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
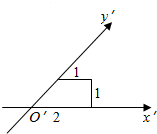
| A. | $\frac{3}{2}$ | B. | 3 | C. | $3\sqrt{2}$ | D. | $6\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com