练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在正方体ABCD-A1B1C1D1中,若E是A1C1的中点,则直线CE与BD的位置关系是　　　.

     

    垂直

    【解析】建立空间直角坐标系,利用坐标法解决.

    以A为原点,AB,AD,AA1所在直线分别为x,y,z轴建立空间直角坐标系,如图,

    设正方体棱长为1,

    则C(1,1,0),B(1,0,0),D(0,1,0),E(,,1),

    ∴=(-,-,1),=(-1,1,0),

    显然·=-+0=0,

    ∴⊥,即CE⊥BD.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（三）第一章第三节练习卷（解析版） 题型：选择题

    命题“?x∈[1,2],x2-a≤0”为真命题的一个充分而不必要条件是(　　)

    (A)a≥4 (B)a≤4 (C)a≥5 (D)a≤5

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷（解析版） 题型：填空题

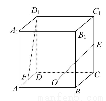
    如图,在棱长为2的正方体ABCD -A1B1C1D1中,点O是底面ABCD的中心,点E,F分别是CC1,AD的中点,则异面直线OE与FD1所成角的余弦值为　　　　.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷（解析版） 题型：填空题

    若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则　　　　(写出所有正确结论的编号).

    ①四面体ABCD每组对棱相互垂直;

    ②四面体ABCD每个面的面积相等;

    ③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°;

    ④连接四面体ABCD每组对棱中点的线段相互垂直平分;

    ⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷（解析版） 题型：选择题

    设l,m,n为三条不同的直线,α,β为两个不同的平面,下列命题中正确的个数是(　　)

    ①若l⊥α,m∥β,α⊥β,则l⊥m;

    ②若m?α,n?α,l⊥m,l⊥n,则l⊥α;

    ③若l∥m,m∥n,l⊥α,则n⊥α;

    ④若l∥m,m⊥α,n⊥β,α∥β,则l∥n.

    (A)1 (B)2 (C)3 (D)4

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷（解析版） 题型：选择题

    已知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的一个单位法向量是(　　)

    (A)(,,-) (B) (,-,) (C)(-,,) (D)(-,-,-)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业四十五第七章第四节练习卷（解析版） 题型：解答题

    如图所示,四边形EFGH所在平面为三棱锥A-BCD的一个截面,四边形EFGH为平行四边形.

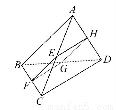
    (1)求证:AB∥平面EFGH,CD∥平面EFGH.

    (2)若AB=4,CD=6,求四边形EFGH周长的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷（解析版） 题型：解答题

    用一个平行于圆锥底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3cm,求圆台的母线长.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷（解析版） 题型：解答题

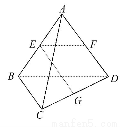
    如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F,G分别是AB,AD,CD的中点,计算:

    (1)·.

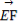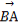    (2)EG的长.

    (3)异面直线EG与AC所成角的大小.

     

    查看答案和解析>>

    同步练习册答案