
【题目】如图,![]() ,
,![]() 为异面直线,且
为异面直线,且![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上两点,
上两点,![]() ,
,![]() 是
是![]() 上两点,
上两点,![]() ,
,![]() ,
,![]() ,
,![]() 分别交
分别交![]() 于点
于点![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)若![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 所成角为
所成角为![]() ,求四边形
,求四边形![]() 的面积.
的面积.
科目:高中数学 来源: 题型:
【题目】设{an}是一个首项为2,公比为q(q![]() 1)的等比数列,且3a1,2a2,a3成等差数列.
1)的等比数列,且3a1,2a2,a3成等差数列.
(1)求{an}的通项公式;
(2)已知数列{bn}的前n项和为Sn,b1=1,且![]() 1(n≥2),求数列{an
1(n≥2),求数列{an![]() bn}的前n项和Tn.
bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的周期为
)的周期为![]() ,图像的一个对称中心为
,图像的一个对称中心为![]() ,将函数
,将函数![]() 图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移
图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图像.
的图像.
(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)是否存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定![]() 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.
(3)求实数a与正整数n,使得![]() 在
在![]() 内恰有2013个零点.
内恰有2013个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四位同学参加三项不同的竞赛.
(1)每位同学必须参加一项,有几种不同结果?
(2)每项竞赛只有且必须有一位同学参加,有几种不同结果?
(3)每位同学最多参加一项,且每项竞赛只许有一位同学参加,有几种不同结果?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对有![]() 个元素的总体
个元素的总体![]() 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体![]() 和
和![]() (m是给定的正整数,且
(m是给定的正整数,且![]() ),再从每个子总体中各随机抽取2个元素组成样本,用
),再从每个子总体中各随机抽取2个元素组成样本,用![]() 表示元素i和j同时出现在样本中的概率,则
表示元素i和j同时出现在样本中的概率,则![]() _________;所有
_________;所有![]() 的和等于________.
的和等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
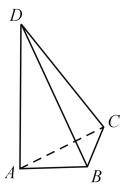
【题目】如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2. 若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
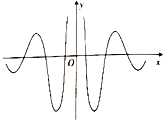
【题目】著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,我们经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如某体育品牌的LOGO为![]() ,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|2x﹣2|的最大值为M,正实数a,b满足a+b=M.
(1)求2a2+b2的最小值;
(2)求证:aabb≥ab.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com