
分析 (Ⅰ)求出抛物线的焦点,结合三角形的周长求出a,b,即可求椭圆C的方程;
(Ⅱ)设出直线方程,联系直线和椭圆,利用根与系数之间的关系进行求解即可.
解答 解:(Ⅰ)依题意得$\left\{\begin{array}{l}c=1\\ 2a+2c=2\sqrt{2}+2\\{a^2}={b^2}+{c^2}\end{array}\right.⇒\left\{\begin{array}{l}{a^2}=2\\{b^2}=1\end{array}\right.$
所以椭圆C的方程$\frac{x^2}{2}+{y^2}=1$….(5分)
(Ⅱ)设A(x1,y1),B(x2,y2)
联立$\left\{\begin{array}{l}y=kx+m\\{x^2}+2{y^2}-2=0\end{array}\right.⇒(1+2{k^2}){x^2}+4kmx+2{m^2}-2=0$,
$\left\{\begin{array}{l}△>0⇒1+2{k^2}>m(*)\\{x_1}+{x_2}=\frac{-4km}{{1+2{k^2}}}\\{x_1}{x_2}=\frac{{2{m^2}-2}}{{1+2{k^2}}}\end{array}\right.$①,设△AOB的重心G(x,y),
由$\overrightarrow{{F_1}G}•\overrightarrow{{F_2}G}=-\frac{5}{9}$可得${x^2}+{y^2}=\frac{4}{9}$②
由重心公式可得$G(\frac{{{x_1}+{x_2}}}{3},\frac{{{y_1}+{y_2}}}{3})$代入②式
整理可得${({x_1}+{x_2})^2}+{({y_1}+{y_2})^2}=4⇒{({x_1}+{x_2})^2}+{[k({x_1}+{x_2})+2m]^2}=4$③
①式带入③式并整理得${m^2}=\frac{{{{(1+2{k^2})}^2}}}{{1+4{k^2}}}$带入(*)得k≠0.
则${m^2}=\frac{{{{(1+2{k^2})}^2}}}{{1+4{k^2}}}=1+\frac{{4{k^4}}}{{1+4{k^2}}}=1+\frac{4}{{\frac{4}{k^2}+\frac{1}{k^4}}}$,
∵$k≠0∴t=\frac{1}{k^2}>0∴{t^2}+4t>0∴{m^2}>1∴m∈(-∞,-1)∪(1,+∞)$….(12分)
点评 本题主要考查椭圆的方程以及直线和椭圆的位置关系的应用,利用消元法转化为一元二次方程形式是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 |
| y=f(x) | 3 | 0 | 1 | 2 |
| x | 0 | 1 | 2 | 3 |
| y=g(x) | 1 | 0 | 3 | 2 |
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
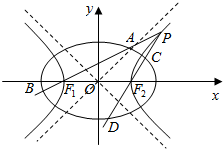 如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),以该椭圆上的异于长轴端点的点和椭圆的左,右焦点F1,F2为顶点的三角形的周长为8$\sqrt{2}$,以椭圆的四个顶点组成的菱形的面积为8$\sqrt{2}$,双曲线G:x2-y2=m(m>0)的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A,B和C,D.
如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),以该椭圆上的异于长轴端点的点和椭圆的左,右焦点F1,F2为顶点的三角形的周长为8$\sqrt{2}$,以椭圆的四个顶点组成的菱形的面积为8$\sqrt{2}$,双曲线G:x2-y2=m(m>0)的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A,B和C,D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率直方图如图所示,已知次数在[100,110)间的频数为7,次数在110以下(不含110)视为不达标,次数在[110,130)视为达标,次数在130以上视为有优秀.
为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率直方图如图所示,已知次数在[100,110)间的频数为7,次数在110以下(不含110)视为不达标,次数在[110,130)视为达标,次数在130以上视为有优秀.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com