
【题目】已知椭圆![]() :
:![]() 和圆
和圆![]() :
:![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,当直线
上,当直线![]() 与圆
与圆![]() 相切时,
相切时,![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,且与椭圆
,且与椭圆![]() 和圆
和圆![]() 都相切,切点分别为
都相切,切点分别为![]() ,
,![]() ,记
,记![]() 和
和![]() 的积分别为
的积分别为![]() 和
和![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(I) 由题意可得![]() ,设
,设![]() ,运用直线和圆相切的条件,可得
,运用直线和圆相切的条件,可得![]() ,结合a,b, c的关系,解得a, c,进而得到椭圆方程;
,结合a,b, c的关系,解得a, c,进而得到椭圆方程;
(Ⅱ)设![]() ,
,![]() ,将
,将![]() 代入
代入![]() ,结合直线和椭圆相切的条件判别式为0,解得M的坐标,可得
,结合直线和椭圆相切的条件判别式为0,解得M的坐标,可得![]() 的面积
的面积![]() ,再由直线和圆相切的条件,解方程可得N的坐标,求得Q的坐标,计算
,再由直线和圆相切的条件,解方程可得N的坐标,求得Q的坐标,计算![]() 的面积为
的面积为![]() ,求得
,求得![]() 的表达式,化简后运用基本不等式即可得证.
的表达式,化简后运用基本不等式即可得证.
(Ⅰ)由题可知![]() . ①
. ①
设![]() ,则由
,则由![]() 与圆相切时
与圆相切时![]() 得
得![]() ,即
,即![]() . ②
. ②
将①②代入![]() 解得
解得![]() .
.
所以![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,
将![]() 代入
代入![]() 得
得![]() ,
,
由直线![]() 与椭圆
与椭圆![]() 相切得
相切得![]() 即
即![]() ,且
,且
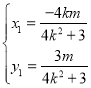 ,
,
则![]() 的面积
的面积![]() .
.
由直线![]() 与圆
与圆![]() 相切,设
相切,设![]() :
:![]() ,与
,与![]() 联立得
联立得
 .
.
直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则![]() .
.
则![]() 的面积
的面积![]() ,
,
从而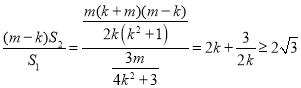 .(当且仅当
.(当且仅当![]() 时等号成立),
时等号成立),
所以![]() 的最小值为
的最小值为![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日![]() 点的轨道运行.
点的轨道运行.![]() 点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,
点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,![]() 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
![]() .
.
设![]() ,由于
,由于![]() 的值很小,因此在近似计算中
的值很小,因此在近似计算中![]() ,则r的近似值为
,则r的近似值为
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖北七市州高三5月23日联考后,从全体考生中随机抽取44名,获取他们本次考试的数学成绩![]() 和物理成绩
和物理成绩![]() ,绘制成如图散点图:
,绘制成如图散点图:
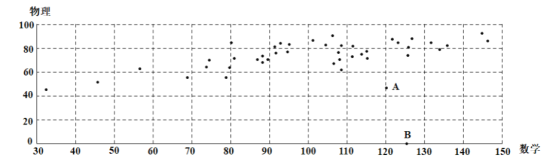
根据散点图可以看出![]() 与
与![]() 之间有线性相关关系,但图中有两个异常点
之间有线性相关关系,但图中有两个异常点![]() .经调查得知,
.经调查得知,![]() 考生由于重感冒导致物理考试发挥失常,
考生由于重感冒导致物理考试发挥失常,![]() 考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计的值:
考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计的值:![]()
![]()
![]() 其中
其中![]() ,
,![]() 分别表示这42名同学的数学成绩、物理成绩,
分别表示这42名同学的数学成绩、物理成绩,![]() ,2,…,42,
,2,…,42,![]() 与
与![]() 的相关系数
的相关系数![]() .
.
(1)若不剔除![]() 两名考生的数据,用44组数据作回归分析,设此时
两名考生的数据,用44组数据作回归分析,设此时![]() 与
与![]() 的相关系数为
的相关系数为![]() .试判断
.试判断![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)求![]() 关于
关于![]() 的线性回归方程,并估计如果
的线性回归方程,并估计如果![]() 考生参加了这次物理考试(已知
考生参加了这次物理考试(已知![]() 考生的数学成绩为125分),物理成绩是多少?
考生的数学成绩为125分),物理成绩是多少?
(3)从概率统计规律看,本次考试七市州的物理成绩![]() 服从正态分布
服从正态分布![]() ,以剔除后的物理成绩作为样本,用样本平均数
,以剔除后的物理成绩作为样本,用样本平均数![]() 作为
作为![]() 的估计值,用样本方差
的估计值,用样本方差![]() 作为
作为![]() 的估计值.试求七市州共50000名考生中,物理成绩位于区间(62.8,85.2)的人数
的估计值.试求七市州共50000名考生中,物理成绩位于区间(62.8,85.2)的人数![]() 的数学期望.
的数学期望.
附:①回归方程![]() 中:
中: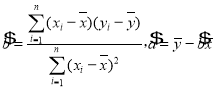
②若![]() ,则
,则![]()
③![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).设
为参数).设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时,![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的普通方程;
的普通方程;
(2)设![]() 为圆
为圆![]() 上任意一点,求
上任意一点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
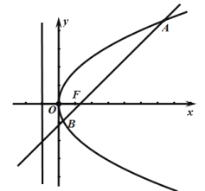
【题目】已知抛物线![]() 的焦点
的焦点![]() 到准线
到准线![]() 的距离为2,直线
的距离为2,直线![]() 与抛物线交于不同的两点
与抛物线交于不同的两点![]() ,
,![]() .
.
(1)求抛物线的方程;
(2)是否存在与![]() 的取值无关的定点
的取值无关的定点![]() ,使得直线
,使得直线![]() ,
,![]() 的斜率之和恒为定值?若存在,求出所有点
的斜率之和恒为定值?若存在,求出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共l4分)
已知函数f(x)=![]() x +
x +![]() , h(x)=
, h(x)=![]() .
.
(I)设函数F(x)=f(x)一h(x),求F(x)的单调区间与极值;
(Ⅱ)设a∈R,解关于x的方程log4[![]() ]=1og2h(a-x)一log2h (4-x);
]=1og2h(a-x)一log2h (4-x);
(Ⅲ)试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点O为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:
轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:![]() ,曲线C2的参数方程为:
,曲线C2的参数方程为: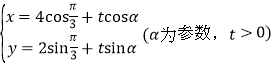 ,点N的极坐标为
,点N的极坐标为![]() .
.
(Ⅰ)若M是曲线C1上的动点,求M到定点N的距离的最小值;
(Ⅱ)若曲线C1与曲线C2有有两个不同交点,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂新购置甲、乙两种设备,分别生产A,B两种产品,为了解这两种产品的质量,随机抽取了200件进行质量检测,得到质量指标值的频数统计表如下:
质量指标值 |
|
|
|
|
|
| 合计 |
A产品频数 | 2 | 6 | a | 32 | 20 | 10 | 80 |
B产品频数 | 12 | 24 | b | 27 | 15 | 6 | n |
产品质量2×2列联表
产品质量高 | 产品质量一般 | 合计 | |
A产品 | |||
B产品 | |||
合计 |
附: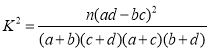
|
|
|
|
|
|
|
|
(1)求a,b,n的值,并估计A产品质量指标值的平均数;
(2)若质量指标值大于50,则说明该产品质量高,否则说明该产品质量一般.请根据频数表完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为质量高低与引入甲、乙设备有关.
的把握认为质量高低与引入甲、乙设备有关.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com