
分析 如图所示,直线l与AB1所成角即为∠B1AC.利用余弦定理,可得结论.
解答 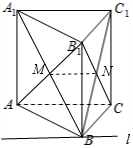 解:如图所示,直线l与AB1所成角即为∠B1AC.
解:如图所示,直线l与AB1所成角即为∠B1AC.
设三棱柱的棱长为a,B1A=B1C=$\sqrt{2}$a,AC=a,
∴cos∠B1AC=$\frac{2{a}^{2}+{a}^{2}-2{a}^{2}}{2•\sqrt{2}a•a}$=$\frac{\sqrt{2}}{4}$,
∴直线l与AB1所成角的余弦值为$\frac{\sqrt{2}}{4}$.
故答案为:$\frac{\sqrt{2}}{4}$.
点评 本题考查直线l与AB1所成角,考查余弦定理,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
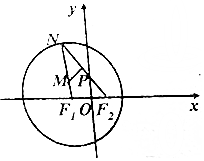 已知F1为圆(x+1)2+y2=16的圆心,N为圆F1上一动点,且F2(1,0),点M,P分别是线段F1N,F2N上的点,满足$\overrightarrow{MP}$•$\overrightarrow{{F}_{2}N}$=0,$\overrightarrow{{F}_{2}N}$=2$\overrightarrow{{F}_{2}P}$.
已知F1为圆(x+1)2+y2=16的圆心,N为圆F1上一动点,且F2(1,0),点M,P分别是线段F1N,F2N上的点,满足$\overrightarrow{MP}$•$\overrightarrow{{F}_{2}N}$=0,$\overrightarrow{{F}_{2}N}$=2$\overrightarrow{{F}_{2}P}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 我国古代的劳动人民曾创造了灿烂的中华文明,戍边的官兵通过在烽火台上举火向国内报告,烽火台上点火表示数字1,不点火表示数字0,这蕴含了进位制的思想.下面程序框图的算法思路就源于我国古代戍边官兵的“烽火传信”.执行该程序框图,若输入a=1234,k=5,n=4则输出的b=( )
我国古代的劳动人民曾创造了灿烂的中华文明,戍边的官兵通过在烽火台上举火向国内报告,烽火台上点火表示数字1,不点火表示数字0,这蕴含了进位制的思想.下面程序框图的算法思路就源于我国古代戍边官兵的“烽火传信”.执行该程序框图,若输入a=1234,k=5,n=4则输出的b=( )| A. | 26 | B. | 194 | C. | 569 | D. | 819 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{π}{2}$,-$\frac{π}{4}$) | B. | (0,$\frac{π}{2}$) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{3π}{2}$,2π) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
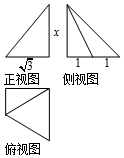 某几何体的三视图如图所示,且该几何体的体积是$\sqrt{3}$cm3,则正视图中的x值是2cm,该几何体的表面积是$\frac{{5\sqrt{3}+3\sqrt{7}+4}}{2}$cm2.
某几何体的三视图如图所示,且该几何体的体积是$\sqrt{3}$cm3,则正视图中的x值是2cm,该几何体的表面积是$\frac{{5\sqrt{3}+3\sqrt{7}+4}}{2}$cm2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com