
 在五面体ABCDEF中,AB∥CD∥EF,CD=EF=CF=2AB=2AD=2,∠DCF=60°,AD⊥CD,平面CDEF⊥平面ABCD.
在五面体ABCDEF中,AB∥CD∥EF,CD=EF=CF=2AB=2AD=2,∠DCF=60°,AD⊥CD,平面CDEF⊥平面ABCD.分析 (1)证明一条直线垂直一个平面,只需要证明这条两个平面垂直,直线垂直两个平面的交线即可.证明CE⊥DF
∵平面CDEF⊥平面ABCD,平面CDEF∩平面ABCD=CD,CE⊥AD,即可得到直线CE⊥平面ADF.
(2)根据题意,取EF的中点G,证明DA,DC,DG两两垂直.以D为原点,DA,DC,DG的方向为x,y,z轴,建立空间直角坐标系,进行计算,确定P在棱BC上的位置.
解答 证明:(1)∵CD∥EF,CD=EF=CF=2,∴四边形CDEF为菱形,
∴CE⊥DF
∵平面CDEF⊥平面ABCD,平面CDEF∩平面ABCD=CD,
∵AD⊥CD,∴AD⊥平面ACDEF,
∴CE⊥AD,又∵AD∩DF=D,∴直线CE⊥平面ADF;
解:(2)∵∠DCF=60°,∴△DEF为正三角形,取EF的中点G,连接GD,则GD⊥EF,∴GD⊥CD.
∵平面CDEF⊥平面ABCD,GD?平面CDEF,平面CDEF∩平面ABCD=CD,
∴GD⊥平面ABCD.∵AD⊥CD,∴DA,DC,DG两两垂直.
以D为原点,DA,DC,DG的方向为x,y,z轴,建立空间直角坐标系.
∵CD=EF=CF=2,AB=AD=1,∴$E(0,-1,\sqrt{3}),F(0,1,\sqrt{3})$,
由(1)知$\overrightarrow{CE}=(0,-3,\sqrt{3})$是平面ADF的法向量.∵$\overrightarrow{DF}=(0,1,\sqrt{3})$,$\overrightarrow{CB}=(1,-1,0)$,
设$\overrightarrow{CP}=a\overrightarrow{CB}=(a,-a,0)$,$\overrightarrow{DP}=\overrightarrow{DC}+\overrightarrow{CP}=(a,2-a,0)$,
设平面PDF的法向量为$\overrightarrow n=(x,y,z)$,∵$\overrightarrow n•\overrightarrow{DF}=0$,$\overrightarrow n•\overrightarrow{DP}=0$,
∴$\left\{{\begin{array}{l}{y+\sqrt{3}z=0}\\{ax+(2-a)y=0}\end{array}}\right.$,令$y=\sqrt{3}a$,则$x=\sqrt{3}(a-2),z=-a$,
∴$\overrightarrow n=(\sqrt{3}(a-2),\sqrt{3}a,-a)$.
∵二面角P-DF-A为60°,
∴$|{cos<\overrightarrow n,\overrightarrow{CE}>}|=\frac{{|{\overrightarrow n•\overrightarrow{CE}}|}}{{|{\overrightarrow n}||{\overrightarrow{CE}}|}}=\frac{{4a\sqrt{3}}}{{\sqrt{12}\sqrt{3{{(a-2)}^2}}+3{a^2}+{a^2}}}=\frac{1}{2}$,解得$a=\frac{2}{3}$.
∴P点在靠近B点的CB的三等分点处.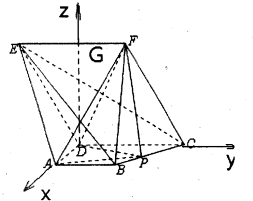
点评 本题考查了线面垂直的证明方法.线面垂直可以转化成证明面面垂直,也可以证明直线垂直平面内的两条相交直线.同时考查了空间直角坐标系在立体几何中的运用能力和计算能力!属于难题.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:选择题
| A. | 335 | B. | 337 | C. | 1 678 | D. | 2 017 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
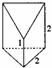 如图是底面边长为2,高为2的正三棱柱除去上面的一个高为1的三棱锥后剩下的部分构成的几何体的直观图,则该几何体的体积为$\frac{5\sqrt{3}}{3}$.
如图是底面边长为2,高为2的正三棱柱除去上面的一个高为1的三棱锥后剩下的部分构成的几何体的直观图,则该几何体的体积为$\frac{5\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+2x+1=0 | B. | ?x∈R,-$\sqrt{x+1}$≥0 | ||
| C. | ?x∈N*,log2x>0 | D. | ?x∈R,cosx<2x-x2-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
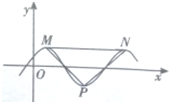 函数f(x)=$\frac{1}{2}$sin($\frac{1}{2}$ωx+$\frac{π}{6}$)(ω>0,)x∈R的部分图象如图所示,设M,N是图象上的最高点,P是图象上的最低点,若△PMN为等腰直角三角形,则ω=2π.
函数f(x)=$\frac{1}{2}$sin($\frac{1}{2}$ωx+$\frac{π}{6}$)(ω>0,)x∈R的部分图象如图所示,设M,N是图象上的最高点,P是图象上的最低点,若△PMN为等腰直角三角形,则ω=2π.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com