
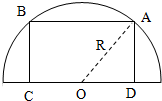
 在一个圆心为O,半径为R半圆形钢板上截取一块矩形材料,怎样截取能使这个矩形的面积最大?
在一个圆心为O,半径为R半圆形钢板上截取一块矩形材料,怎样截取能使这个矩形的面积最大? 分析 设∠AOB=θ且θ为锐角,半圆的半径为R,用θ参数表示出矩形的面积S=R2sin(2∠BOA).再求出S的最大值即可.
解答 解:设∠AOB=θ且θ为锐角,半圆的半径为R,则|AB|=Rsinθ
DA=2|AO|=2Rcosθ
∴这个矩形的面积为:S=2Rcos∠BOA×Rsin∠BOA=R2sin(2∠BOA)
因此当sin(2∠BOA)=1时,S最大.
即∠BOA=$\frac{π}{4}$时,矩形面积最大,最大为R2
也就是当AD=$\sqrt{2}R$,AB=$\frac{\sqrt{2}R}{2}$时矩形面积最大
故当AD=$\sqrt{2}R$,AB=$\frac{\sqrt{2}R}{2}$时矩形面积最大.
点评 本题主要考查了带参数的三角形面积公式,三角函数的最值等知识点,属中档题.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(1,2)∪(3,+∞) | B. | (-1,1)∪(2,3) | C. | (-1,1)∪(1,2) | D. | (1,2)∪(2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-$\frac{1}{3}$)>f($\frac{5}{2}$) | B. | f(-$\frac{1}{3}$)<f($\frac{5}{2}$) | C. | f(-$\frac{1}{3}$)=f($\frac{5}{2}$) | D. | f(-$\frac{1}{3}$)<f($\frac{9}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com