
分析 (1)设C点坐标为(x,y),根据中点坐标公式,得到A点坐标为(2x,0),B点坐标为(0,2y),由|AB|=2,即可求出曲线C1的方程,
(2)先求出,△COD是等腰直角三角形,|CD|=$\sqrt{2}$,再根据点到直线的距离公式得到$\frac{1}{\sqrt{2{a}^{2}+{b}^{2}}}$=$\frac{\sqrt{2}}{2}$,再由点到点的距离公式,根据函数的性质即可求出.
解答 解:(1)设C点坐标为(x,y),则A点坐标为(2x,0),B点坐标为(0,2y),由|AB|=2,得(2x-0)2+(0-2y)2=4,
化简得x2+y2=1,
所以曲线C1的方程x2+y2=1,
(2)由曲线C1的方程x2+y2=1可知圆心(0,0),半径为1,
所以|OC|=|OD|=1,△COD是等腰直角三角形,|CD|=$\sqrt{2}$,
圆心(0,0)到直线$\sqrt{2}$ax+by=1的距离$\frac{1}{\sqrt{2{a}^{2}+{b}^{2}}}$=$\frac{\sqrt{2}}{2}$,
即2a2+b2=2,
所以a2=1-$\frac{1}{2}$b2,(-$\sqrt{2}$≤b≤$\sqrt{2}$)
点P(a,b)与点(0,1)之间距离|OP|=$\sqrt{{a}^{2}+(b-1)^{2}}$=$\sqrt{1-\frac{1}{2}{b}^{2}+(b-1)^{2}}$=$\sqrt{\frac{1}{2}{b}^{2}-2b+2}$=$\sqrt{\frac{1}{2}(b-2)^{2}}$,
当b=$\sqrt{2}$时,|OP|取到最小值|OP|=$\sqrt{3-2\sqrt{2}}$=$\sqrt{2}$-1.
点评 本题考查了点的轨迹方程,点到直线的距离,点到点的距离,以及函数的性质,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
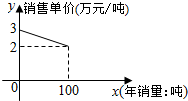 某种产品的成本f1(x)(万元)与年产量x(吨)之间的函数关系是f1(x)=$\frac{1}{100}$x2,该产品的销售单价f2(x)可以表示为关于年销量的一次函数,其部分图象如图所示,且生产的产品都能在当年销售完.
某种产品的成本f1(x)(万元)与年产量x(吨)之间的函数关系是f1(x)=$\frac{1}{100}$x2,该产品的销售单价f2(x)可以表示为关于年销量的一次函数,其部分图象如图所示,且生产的产品都能在当年销售完.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆的面积与半径具有相关性 | B. | 纯净度与净化次数不具有相关性 | ||
| C. | 作物的产量与人的耕耘是负相关 | D. | 学习成绩与学习效率是正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,${x}_{0}^{2}$+2x0≤2 | B. | ?x∈R,x2+2x≥2 | ||
| C. | ?x0∈R,${x}_{0}^{2}$+2x0<2 | D. | ?x∈R,x2+2x<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y′=-exsinx | B. | y′=ex-sinx | C. | y′=$\sqrt{2}$exsin(x+$\frac{π}{4}$) | D. | y′=$\sqrt{2}$exsin($\frac{π}{4}$-x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
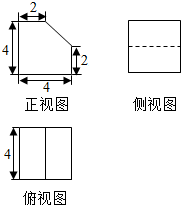
| A. | 84 | B. | $76+8\sqrt{2}$ | C. | $78+8\sqrt{2}$ | D. | $80+8\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com