
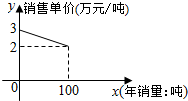
 某种产品的成本f1(x)(万元)与年产量x(吨)之间的函数关系是f1(x)=$\frac{1}{100}$x2,该产品的销售单价f2(x)可以表示为关于年销量的一次函数,其部分图象如图所示,且生产的产品都能在当年销售完.
某种产品的成本f1(x)(万元)与年产量x(吨)之间的函数关系是f1(x)=$\frac{1}{100}$x2,该产品的销售单价f2(x)可以表示为关于年销量的一次函数,其部分图象如图所示,且生产的产品都能在当年销售完.分析 (1)由题意可设:f2(x)=kx+b(k≠0),由于图象经过点(0,3),(100,2).代入解出即可得出.令f2(x)>0,解得函数的定义域.
(2)设年产量为x吨,s=x•f2(x)-f1(x)=-$\frac{1}{50}$(x-75)2+$\frac{225}{2}$,利用二次函数的单调性即可得出.
解答 解:(1)由题意可设:f2(x)=kx+b(k≠0),由于图象经过点(0,3),(100,2).
∴$\left\{\begin{array}{l}{3=b}\\{2=100k+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{100}}\\{b=3}\end{array}\right.$,
∴f2(x)=$-\frac{1}{100}x$+3,令f2(x)=$-\frac{1}{100}x$+3>0,解得0<x<300,其定义域为(0,300).
(2)设年产量为x吨,s=x•f2(x)-f1(x)=$x(-\frac{1}{100}x+3)$-$\frac{1}{100}$x2=$-\frac{1}{50}{x}^{2}$+3x=-$\frac{1}{50}$(x-75)2+$\frac{225}{2}$,
∴当x=75时,s取得最大值$\frac{225}{2}$(万元).
点评 本题考查了一次函数与二次函数的图象与性质,考查了推理能力与计算能力,属于中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b | B. | a$<\frac{b}{2}$ | C. | a$>\frac{b}{2}$ | D. | a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{4}$ | B. | -2 | C. | -$\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①简单随机抽样,②分层抽样,③系统抽样 | |
| B. | ①简单随机抽样,②系统抽样,③分层抽样 | |
| C. | ①系统抽样,②简单随机抽样,③分层抽样 | |
| D. | ①分层抽样,②系统抽样,③简单随机抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com