
分析 写出原命题的否定,可判断①;根据虚数单位的定义,可判断②;判断原命题的逆否命题的真假,可判断③;根据圆锥的几何特征,可判断④.
解答 解:①命题“存在${x_0}∈R,{2^{x_0}}≤0$”的否定是“?${x_0}∈R,{2^{x_0}}>0$”,故为假命题;
②若z是纯虚数,不妨令z=bi(b≠0),则z2=-b2<0,故为真命题;
③若x+y≠3,则x≠2或y≠1的逆否命题为:若x=2且y=1,则x+y=3为真命题,故原命题也为真命题;
④以直角三角形的直角边为旋转轴,旋转一周所得的旋转体才是圆锥,故为假命题;
故答案为:②③
点评 本题考查的知识点是特称命题,算数,四种命题,圆锥的几何特征,难度中档.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
| 部门 | 高中部 | 初中部 | 小学部 | 幼教部 |
| 人数 | 4 | 4 | 2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
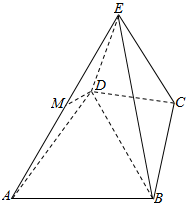 如图几何体E-ABCD是四棱锥,△ABD为正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD.
如图几何体E-ABCD是四棱锥,△ABD为正三角形,∠BCD=120°,CB=CD=CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com