
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度后,再将所得的图象向下平移一个单位长度得到函数
个单位长度后,再将所得的图象向下平移一个单位长度得到函数![]() 的图象,且
的图象,且![]() 的图象与直线
的图象与直线![]() 相邻两个交点的距离为
相邻两个交点的距离为![]() ,若
,若![]() 对任意
对任意![]() 恒成立,则
恒成立,则![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N-BCM的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于某产品的明星代言费![]() (百万元)和其销售额
(百万元)和其销售额![]() (百万元),有如下表的统计表格:
(百万元),有如下表的统计表格:
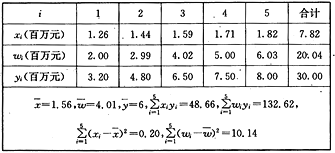
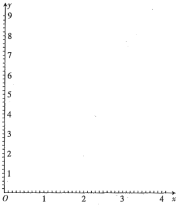 表中
表中![]()
(1)在给出的坐标系![]() 中,作出销售额
中,作出销售额![]() 关于广告费
关于广告费![]() 的回归方程的散点图,根据散点图指出:
的回归方程的散点图,根据散点图指出:![]() 哪一个适合作销售额
哪一个适合作销售额![]() 关于明星代言费
关于明星代言费![]() 的回归方程(不需要说明理由);并求
的回归方程(不需要说明理由);并求![]() 关于
关于![]() 的回归方程(结果精确到0.1)
的回归方程(结果精确到0.1)
(2)已知这种产品的纯收益![]() (百万元)与
(百万元)与![]() ,
,![]() 有如下关系:
有如下关系:![]() ,用(1)中的结果估计当
,用(1)中的结果估计当![]() 取何值时,纯收益
取何值时,纯收益![]() 取最大值?
取最大值?
附:对于一组数据![]() 其回归线
其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为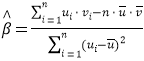 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,若函数
时,若函数![]() 的导函数
的导函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,其横坐标分别为
两点,其横坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,且
,且![]() ,
, ![]() 恰为函数
恰为函数![]() 的零点,求证:
的零点,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,若直线
轴的非负半轴为极轴建立极坐标系,若直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,过
,过![]() 的直线与直线
的直线与直线![]() 平行,且与曲线
平行,且与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若 ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表为2015年至2018年某百货零售企业的年销售额![]() (单位:万元)与年份代码
(单位:万元)与年份代码![]() 的对应关系,其中年份代码
的对应关系,其中年份代码![]() 年份-2014(如:
年份-2014(如:![]() 代表年份为2015年)。
代表年份为2015年)。
年份代码 | 1 | 2 | 3 | 4 |
年销售额 | 105 | 155 | 240 | 300 |
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测2019年该百货零售企业的年销售额;
的线性回归方程,并预测2019年该百货零售企业的年销售额;
(2)2019年,美国为遏制我国的发展,又祭出“长臂管辖”的霸权行径,单方面发起对我国的贸易战,有不少人对我国经济发展前景表示担忧.此背景下,某调查平台为了解顾客对该百货零售企业的销售额能否持续增长的看法,随机调查了60为男顾客、50位女顾客,得到如下![]() 列联表:
列联表:
持乐观态度 | 持不乐观态度 | 总计 | |
男顾客 | 45 | 15 | 60 |
女顾客 | 30 | 20 | 50 |
总计 | 75 | 35 | 110 |
问:能否在犯错误的概率不超过0.05的前提下认为对该百货零售企业的年销售额持续增长所持的态度与性别有关?
参考公式及数据:回归直线方程 ,
,
![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 甲、乙二人比赛,甲胜的概率为![]() ,则比赛5场,甲胜3场
,则比赛5场,甲胜3场
B. 某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人一定治愈
C. 随机试验的频率与概率相等
D. 天气预报中,预报明天降水概率为90%,是指降水的可能性是90%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆方程;
(2)斜率为![]() 的直线
的直线![]() 过点F,且与椭圆交于
过点F,且与椭圆交于![]() 两点,P为直线
两点,P为直线![]() 上的一点,
上的一点,
若![]() 为等边三角形,求直线
为等边三角形,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com