
分析 (Ⅰ)设圆C的方程为(x-a)2+(y-b)2=r2,由已知列关于a,b,r的方程组求解方程组可得a,b,r的值,则圆C的方程可求;
(Ⅱ)(i)直接利用切割线定理求得$\overrightarrow{AM}•\overrightarrow{AN}$的值;
(ii)依题意可知,直线l的方程为y=kx+1,设M(x1,y1),N(x2,y2),把y=kx+1代入(x-2)2+(y-3)2=1并整理,利用根与系数的关系求出A,B的横坐标的和与积,代入$\overrightarrow{OM}•\overrightarrow{ON}=12$求得k值,从而求得直线l的方程.
解答 解:(Ⅰ)设圆C的方程为(x-a)2+(y-b)2=r2,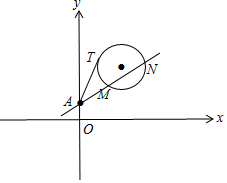
则依题意,得$\left\{\begin{array}{l}{(2-a)^2}+{(4-b)^2}={r^2}\\{(1-a)^2}+{(3-b)^2}={r^2}\\ a-b+1=0\end{array}\right.$,解得$\left\{\begin{array}{l}a=2\\ b=3\\ r=1\end{array}\right.$.
∴圆C的方程为(x-2)2+(y-3)2=1;
(Ⅱ)(i)$\overrightarrow{AM}•\overrightarrow{AN}$为定值.
过点A(0,1)作直线AT与圆C相切,切点为T,则AT2=7,
∴$\overrightarrow{AM}•\overrightarrow{AN}=|\overrightarrow{AM}|•|\overrightarrow{AN}|cos0°=A{T^2}=7$,∴$\overrightarrow{AM}•\overrightarrow{AN}$为定值,且定值为7;
(ii)依题意可知,直线l的方程为y=kx+1,
设M(x1,y1),N(x2,y2),
将y=kx+1代入(x-2)2+(y-3)2=1并整理得:(1+k2)x2-4(1+k)x+7=0,
∴${x_1}+{x_2}=\frac{{4(1+{k^2})}}{{1+{k^2}}}$,${x_1}+{x_2}=\frac{7}{{1+{k^2}}}$,
∴$\overrightarrow{OM}•\overrightarrow{ON}$=x1x2+y1y2=$(1+{k^2}){x_1}{x_2}+k({x_1}+{x_2})+1=\frac{4k(1+k)}{{1+{k^2}}}+8=12$,
即$\frac{4k(1+k)}{{1+{k^2}}}=4$,解得k=1,
又当k=1时△>0,∴k=1,
∴直线l的方程为y=x+1.
点评 本题考查利用待定系数法求圆的方程,考查直线与圆位置关系的应用,体现了“设而不求”的解题思想方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4+$\sqrt{2}$+$\sqrt{6}$ | B. | 3+$\sqrt{2}$+$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 3+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
| 物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
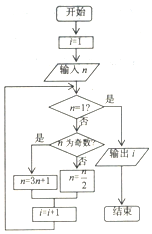 20世纪70年代,流行一种游戏---角谷猜想,规则如下:任意写出一个自然数n,按照以下的规律进行变换:如果n是个奇数,则下一步变成3n+1;如果n是个偶数,则下一步变成$\frac{n}{2}$,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4-2-1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( )
20世纪70年代,流行一种游戏---角谷猜想,规则如下:任意写出一个自然数n,按照以下的规律进行变换:如果n是个奇数,则下一步变成3n+1;如果n是个偶数,则下一步变成$\frac{n}{2}$,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4-2-1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( )| A. | 5 | B. | 16 | C. | 5或32 | D. | 4或5或32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
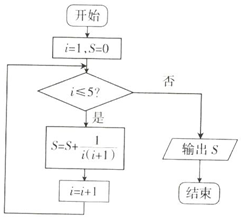
| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{7}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com