
(本小题满分12分)
如图,ABCD为梯形,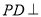 平面ABCD,AB//CD,
平面ABCD,AB//CD,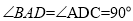
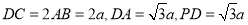 ,E为BC中点
,E为BC中点
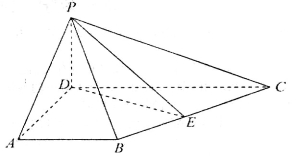
(I)求证:平面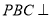 平面PDE;
平面PDE;
(II)线段PC上是否存在一点F,使PA//平面BDF?若有,请找出具体位置,并进行证明;若无,请分析说明理由.
(1)见解析;(2)见解析
【解析】
试题分析:(1)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键;(2) 连结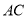 ,
, 相交于点
相交于点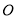 ,根据
,根据 可得
可得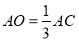 ,然后结合直线与平面平行的判定定理可知在线段
,然后结合直线与平面平行的判定定理可知在线段 上存在一点
上存在一点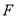 ,使得
,使得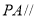 平面
平面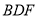 .
.
试题解析:证明:(Ⅰ) 连结

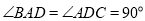 ,
,
所以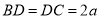 ,
,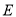 为
为 中点
中点
所以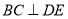 3分
3分
又因为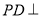 平面
平面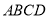 ,
,
所以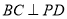
因为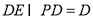 4分
4分
所以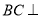 平面
平面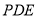 5分
5分
因为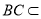 平面
平面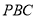 ,所以平面
,所以平面 平面
平面 6分
6分
(Ⅱ)当点 位于
位于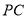 三分之一分点(靠近
三分之一分点(靠近 点)时,
点)时, 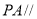 平面
平面 7分
7分
连结 交于
交于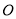 点,
点,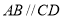 ,所以
,所以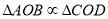

所以 中,
中,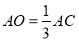 10分
10分
而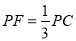
所以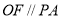 11分
11分
而 平面
平面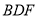
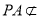 平面
平面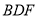
所以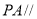 平面
平面 12分
12分
考点:空间几何的位置关系.


科目:高中数学 来源:2014-2015学年四川省资阳市高三第二次诊断性考理科数学试卷(解析版) 题型:选择题
已知 a、b为平面向量,若a+b与a的夹角为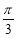 ,a+b与b的夹角为
,a+b与b的夹角为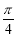 ,则
,则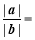 ( )
( )
(A) 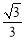 (B)
(B)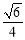
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高三上学期期末考试理科数学试卷B卷(解析版) 题型:解答题
某公司生产甲、乙两种桶装产品,已知生产甲产品1桶需耗A原料3千克,B原料1千克;生产乙产品1桶需耗A原料1千克,B原料3千克.每生产一桶甲产品的利润400元,每生产一桶乙产品的利润300元.公司在生产这两种产品的计划中,每天消耗A、B原料都不超过12千克,通过合理安排生产计划,公司每天可获得的最大利润是(单位:元)
A.1600 B.2100 C.2800 D.4800
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省青岛市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
一个几何体的的三视图如右图所示,则该几何体的体积为

A. 2 B.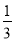 C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省青岛市高三上学期期末考试理科数学试卷(解析版) 题型:选择题
已知函数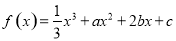 有两个极值点
有两个极值点 ,则直线
,则直线 的斜率的取值范围是
的斜率的取值范围是
A. 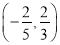 B.
B. 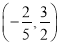 C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省无锡市高三上学期期末考试理科数学试卷(解析版) 题型:填空题
将函数 的图像向左平移个
的图像向左平移个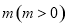 单位长度后,所得的图像关于
单位长度后,所得的图像关于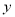 轴对称,则
轴对称,则 的最小值是
的最小值是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com