Question

15．如图，在△ABC中，已知AB=3，AC=6，BC=7，AD是∠BAC平分线．
（1）求证：DC=2BD；
（2）求$\overrightarrow{AB}$$•\overrightarrow{DC}$的值．

Answer 1

分析 （1），过点D作DE∥AB交AC于点E．可得∠EDA=∠DAB，∠EDA=∠EAD，EA=ED．再利用DE∥AB，$\frac{DE}{AB}$=$\frac{CE}{AC}$，$\frac{CD}{DB}$=$\frac{CE}{EA}$即可．
（2）由余弦定理可得，cosA=$\frac{A{C}^{2}+A{B}^{2}-B{C}^{2}}{2AC•AB}$=-$\frac{1}{9}$
$\overrightarrow{AB}$$•\overrightarrow{DC}$=$\overrightarrow{AB}•\frac{2}{3}\overrightarrow{BC}$=$\frac{2}{3}\overrightarrow{AB}•（\overrightarrow{AC}-\overrightarrow{AB}）$=$\frac{2}{3}\overrightarrow{AB}•\overrightarrow{AC}$$-\frac{2}{3}{\overrightarrow{AB}}^{2}$即可．

解答 解：（1）：证明：如图所示，
过点D作DE∥AB交AC于点E．
则∠EDA=∠DAB，又∠DAB=∠EAD，
∴∠EDA=∠EAD，
∴EA=ED．
∵DE∥AB，
∴$\frac{DE}{AB}$=$\frac{CE}{AC}$，即$\frac{AC}{AB}$=$\frac{CE}{DE}=\frac{2}{1}$
∴$\frac{CD}{DB}$=$\frac{CE}{EA}$=$\frac{2}{1}$．
∴DC=2BD；
（2）由余弦定理可得，cosA=$\frac{A{C}^{2}+A{B}^{2}-B{C}^{2}}{2AC•AB}$=-$\frac{1}{9}$
$\overrightarrow{AB}$$•\overrightarrow{DC}$=$\overrightarrow{AB}•\frac{2}{3}\overrightarrow{BC}$=$\frac{2}{3}\overrightarrow{AB}•（\overrightarrow{AC}-\overrightarrow{AB}）$
=$\frac{2}{3}\overrightarrow{AB}•\overrightarrow{AC}$$-\frac{2}{3}{\overrightarrow{AB}}^{2}$
=$\frac{2}{3}×3×6×（-\frac{1}{9}）-\frac{2}{3}×3×3$=-$\frac{22}{3}$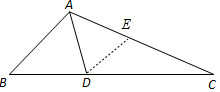

点评 本题主要考查余弦定理和向量数量积的应用．向量和三角函数的综合题是高考热点，要给予重视．