
已知向量 ,
,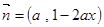 ,其中
,其中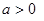 .函数
.函数 在区间
在区间 上有最大值为4,设
上有最大值为4,设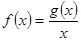 .
.
(1)求实数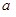 的值;
的值;
(2)若不等式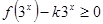 在
在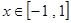 上恒成立,求实数
上恒成立,求实数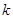 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:解答题
设函数f(x)=ax2+bx+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的零点;
(2)若对任意b∈R,函数f(x)恒有两个不同零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 是正数,
是正数, ,
, ,
, .
.
(Ⅰ)若 成等差数列,比较
成等差数列,比较 与
与 的大小;
的大小;
(Ⅱ)若 ,则
,则 三个数中,哪个数最大,请说明理由;
三个数中,哪个数最大,请说明理由;
(Ⅲ)若 ,
, ,
, (
( ),且
),且 ,
, ,
, 的整数部分分别是
的整数部分分别是

 求所有
求所有 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
己知函数f(x)=ex,x R.
R.
(1)若直线y=kx+1与f(x)的反函数图象相切,求实数k的值;
(2)设x﹥0,讨论曲线y=f(x)与曲线y=mx2(m﹥0)公共点的个数;
(3)设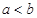 ,比较
,比较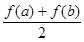 与
与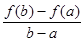 的大小并说明理由。
的大小并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了在夏季降温和冬季供暖时减少能源消耗,房屋的屋顶和外墙需要建造隔热层,某栋建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度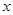 (单位:
(单位: )满足关系:
)满足关系:
若不建隔热层,每年能源消耗费用为8万元。设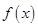 为隔热层建造费用与20年的能源消耗费用之和。
为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求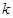 的值及
的值及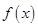 的表达式;
的表达式;
(Ⅱ)隔热层修建多厚时,总费用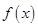 最小,并求最小值.
最小,并求最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com