
分析 由①可推得f(x)=m(x-3m)(x+m+3)<0在x≥1时恒成立,建立关于m的不等式组可得m的范围,然后由②可得:?x∈(-∞,-4),使(x-3m)(x+m+3)<0成立,只要使-4比3m,-m-3中较小的一个大即可,分类讨论可得m的范围,综合可得答案.
解答 解:∵g(x)=2x-4,当x≥2时,g(x)≥0,
又∵?x∈R,f(x)<0或g(x)<0
∴f(x)=m(x-3m)(x+m+3)<0在x≥2时恒成立,
∴二次函数图象开口只能向下,且与x轴交点都在(2,0)的左侧,
即$\left\{\begin{array}{l}m<0\\-m-3<2\\ 3m<2\end{array}\right.$,解得-5<m<0;
又∵?x∈(-∞,-4),f(x)g(x)<0.
而此时有g(x)=2x-4<0.
∴?x∈(-∞,-4),使f(x)=m(x-3m)(x+m+3)>0成立,
由于m<0,∴?x∈(-∞,-4),使(x-3m)(x+m+3)<0成立,
故只要使-4比3m,-m-3中较小的一个大即可,
当m∈(-$\frac{3}{4}$,0)时,3m>-m-3,只要-4>-m-3,解得m>1与m∈(-$\frac{3}{4}$,0)的交集为空集;
当m=-$\frac{3}{4}$时,两根为-2;-2>-4,不符合;
当m∈(-5,-$\frac{3}{4}$)时,3m<-m-3,∴只要-4>3m,解得m<-$\frac{4}{3}$,
综上可得m的取值范围是:(-5,-$\frac{4}{3}$).
点评 此题考查了一元二次不等式的解法,指数函数的单调性及特殊点,利用了分类讨论的思想,分类讨论时要做到不重不漏,考虑问题要全面,是中档题也是易错题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-4)∪(4,+∞) | B. | (-∞,-4)∪(-2,0)∪(2,4) | C. | (-∞,-4)∪(-2,0) | D. | (-4,-2)∪(2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点.在A、P、M、C中任取一点记为E,在B、Q、N、D中任取一点记为F.设G为满足向量$\overrightarrow{OG}$=$\overrightarrow{OE}$+$\overrightarrow{OF}$的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为( )
如图在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点.在A、P、M、C中任取一点记为E,在B、Q、N、D中任取一点记为F.设G为满足向量$\overrightarrow{OG}$=$\overrightarrow{OE}$+$\overrightarrow{OF}$的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为( )| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 49 | B. | 45 | C. | 69 | D. | 73 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
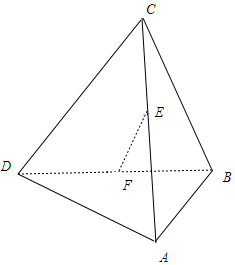
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com