Question

13．空间四边形ABCD中，E、F分别为AC、BD中点，若CD=2AB=2，EF⊥AB，则EF与CD所成的角为（　　）

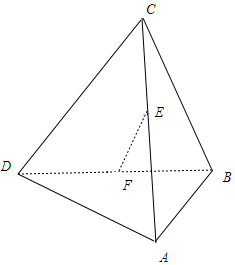
• A． 30°
• B． 45°
• C． 60°
• D． 90°

Answer 1

分析 取AD的中点G，连接EG、FG，由三角形中位线定理得EG∥CD，从而得到∠GEF是EF与CD所成的角，由此能求出EF与CD所成的角的大小．

解答 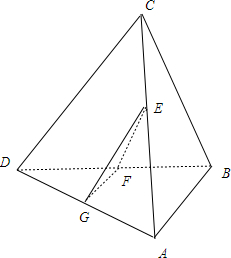解：取AD的中点G，连接EG、FG，
∵E、F分别为AC、BD中点，
∴EG∥CD，且EG=$\frac{1}{2}CD$=1，
FG∥AB，且FG=$\frac{1}{2}AB$=$\frac{1}{2}$．
∵EF⊥AB，FG∥AB，∴EF⊥FG．
∵EG∥CD，∴∠GEF是EF与CD所成的角，
在Rt△EFG中，∵EG=1，GF=$\frac{1}{2}$，EF⊥FG，∴∠GEF=30°，
即EF与CD所成的角为30°．
故选：A．

点评 本题考查的知识点是异面直线及其所成的角，理解异面直线夹角的定义利用平移法，构造出满足条件的平面角是解答的关键．