
已知 椭圆C:
椭圆C: (a>b>0)上任一点P到两个焦点的距离的和为2
(a>b>0)上任一点P到两个焦点的距离的和为2 ,P与椭圆长轴两顶点连线的斜率之积为-
,P与椭圆长轴两顶点连线的斜率之积为- .设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
.设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
(1)若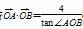 (O为坐标原点),求|y1-y2|的值;
(O为坐标原点),求|y1-y2|的值;
(2)当直线l与两坐标轴都不垂直时,在x轴上是否总存在点Q,使得直线QA,QB的倾斜角互为补角?若存在,求出点Q坐标;若不存在,请说明理由.
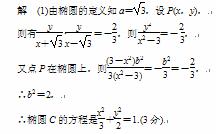
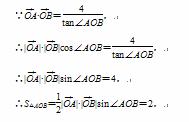 又S△AOB=
又S△AOB=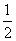 |y1-y2|×1,故|y1-y2|=4.(7分)
|y1-y2|×1,故|y1-y2|=4.(7分)
(2)假设存在一点Q(m,0),使得直线QA,QB的倾斜角互为补角,
依题意可知直线l斜率存在且不为零,
直线l的方程为y=k(x-1)(k≠0),
由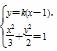 消去y得(3k2+2)x2-6k2x+3k2-6=0,(9分)
消去y得(3k2+2)x2-6k2x+3k2-6=0,(9分)
设A(x1,y1),B(x2,y2),则
∵直线QA,QB的倾斜角互为补角,
∴kQA+kQB=0,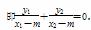
又y1=k(x1-1),y2=k(x2-1),
代入上式可得2x1x2+2m-(m+1)(x1+x2)=0,
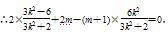 即2m-6=0,∴m=3,
即2m-6=0,∴m=3,
∴存在Q(3,0)使得直线QA,QB的倾斜角互为补角.(16分)


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
某大学教学系共有本科生5 000人,其中一、二、三、四年级的人数比为4∶3∶2∶1, 要
用分层抽样的方法从所有本科生中抽取一个容量为200的样本,则应抽取三年级的学生
人数为( ) A.80 B.60 C.40 D.20
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=aln x= (a为常数
(a为常数 ).
).
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x+2y-5=0垂直,求a的值;
(2)求函数f(x)的单调区间;
(3)当x≥1时,f(x)≤2x-3恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
某商场对A品牌的商品进行了市场调查,预计2012年从1月起前x个月顾客对A品牌的商品的需求总量P(x)件与月份x的近似关系是:
P(x)= x(x+1)(41-2x)(x≤12且x∈N*)
x(x+1)(41-2x)(x≤12且x∈N*)
(1)写出第x月的需求量f(x)的表达式;
(2)若第x月的销售量g(x)=

(单位:件),每件利润q(x)元与月份x的近似关系为:q(x)=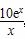 ,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
查看答案和解析>>
科目:高中数学 来源: 题型:
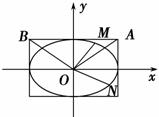
如图,已知椭圆C: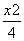 +y2=1,A、B是四条直线x=±2,y=±1所围成的两个顶点.
+y2=1,A、B是四条直线x=±2,y=±1所围成的两个顶点.
(1)设P是椭圆C上任意一点,若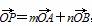 ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
(2)若M、N是椭圆C上两上动点,且直线OM、ON的斜率之积等于直线OA、OB的斜率之积,试探求△OMN的 面积是否为定值,说明理由.
面积是否为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)是定义在R上的偶函数,且当x≥0时,f(x)=(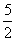 )x,若对任意的x∈[a, a+l],
)x,若对任意的x∈[a, a+l],
不等式f(x+a)≥f2(x)恒成立,则实数a的取值范围是____ 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com