
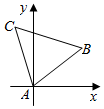
 在平面直角坐标系中,定义两点A(xA,yA),B(xB,yB)间的“L-距离”为d(A-B)=|xA-xB|+|yA-yB|.现将边长为1的正三角形按如图所示方式放置,其中顶点A与坐标原点重合,记边AB所在的直线斜率为k(0≤k≤$\sqrt{3}$),则d(B-C)取得最大值时,边AB所在直线的斜率为2-$\sqrt{3}$.
在平面直角坐标系中,定义两点A(xA,yA),B(xB,yB)间的“L-距离”为d(A-B)=|xA-xB|+|yA-yB|.现将边长为1的正三角形按如图所示方式放置,其中顶点A与坐标原点重合,记边AB所在的直线斜率为k(0≤k≤$\sqrt{3}$),则d(B-C)取得最大值时,边AB所在直线的斜率为2-$\sqrt{3}$. 分析 由题意设B(cosθ,sinθ),则C(cos(θ+$\frac{π}{3}$),sin(θ+$\frac{π}{3}$)),则BC|=|cos(θ+$\frac{π}{3}$)-cosθ|+|sin(θ+$\frac{π}{3}$)-sinθ|,由角的范围化简|BC|,然后利用辅助角公式化积,再利用三角函数求最值得答案.
解答 解:设B(cosθ,sinθ),则C(cos(θ+$\frac{π}{3}$),sin(θ+$\frac{π}{3}$)),
∴|BC|=|cos(θ+$\frac{π}{3}$)-cosθ|+|sin(θ+$\frac{π}{3}$)-sinθ|,
∵0≤θ≤$\frac{π}{3}$,
∴$\frac{π}{3}$≤θ+$\frac{π}{3}$≤$\frac{2π}{3}$<π,即0≤θ<θ+$\frac{π}{3}$<π,
∴|cos(θ+$\frac{π}{3}$)-cosθ|=cosθ-cos(θ+$\frac{π}{3}$).
∵0≤θ≤$\frac{π}{3}$,$\frac{π}{3}$≤θ+$\frac{π}{3}$≤$\frac{2π}{3}$,
∴|sin(θ+$\frac{π}{3}$)-sinθ|=sin(θ+$\frac{π}{3}$)-sinθ,
|BC|=cosθ-cos(θ+$\frac{π}{3}$)+sin(θ+$\frac{π}{3}$)-sinθ
=cosθ-cosθcos$\frac{π}{3}$+sinθsin$\frac{π}{3}$+sinθcos$\frac{π}{3}$+cosθsin$\frac{π}{3}$-sinθ
=$\frac{\sqrt{3}-1}{2}$sinθ+$\frac{\sqrt{3}+1}{2}$cosθ
=$\sqrt{2}$sin(θ+φ)(tanφ=2+$\sqrt{3}$),
由θ+φ=$\frac{π}{2}+$2kπ,k∈Z,得θ=-φ+$\frac{π}{2}+$2kπ,k∈Z,
∴tanθ=tan(-φ+$\frac{π}{2}+$2kπ)=$\frac{1}{tanφ}=\frac{1}{2+\sqrt{3}}=2-\sqrt{3}$,即边AB所在直线的斜率为$2-\sqrt{3}$时,则d(B-C)取得最大值,
故答案为$2-\sqrt{3}$.
点评 本题主要考查三角函数的定义、两角和与差的三角函数公式,考查运算求解能力,考查化归与转化思想,综合性强,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 5 | C. | $\sqrt{13}$ | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是$\frac{7}{8}$.
如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,则$\overrightarrow{BE}$•$\overrightarrow{CE}$的值是$\frac{7}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com