
| A. | (-3,1)∪(3,+∞) | B. | (-3,1)∪(2,+∞) | C. | (-1,1)∪(3,+∞) | D. | (-∞,-1)∪(1,3) |
分析 求出函数值,利用分段函数求解不等式的解集即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{x}^{2}-4x+6,x≥0\\ x+6,x<0\end{array}\right.$,则f(1)=3,
不等式f(x)>f(1)等价于:$\left\{\begin{array}{l}x≥0\\{x}^{2}-4x+6>3\end{array}\right.$或$\left\{\begin{array}{l}x<0\\ x+6>3\end{array}\right.$,
解得:x∈(-3,1)∪(3,+∞).
故选:A.
点评 本题考查分段函数的应用,不等式组的解法,考查计算能力.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| 收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
| A. | 11.4万元 | B. | 11.8万元 | C. | 12.0万元 | D. | 12.2万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知抛物线C1:y=$\frac{1}{4}$x2,圆C2:x2+(y-1)2=1,过点P(t,0)(t>0)作不过原点O的直线PA,PB分别与抛物线C1和圆C2相切,A,B为切点.
如图,已知抛物线C1:y=$\frac{1}{4}$x2,圆C2:x2+(y-1)2=1,过点P(t,0)(t>0)作不过原点O的直线PA,PB分别与抛物线C1和圆C2相切,A,B为切点.查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上文周末检测三数学试卷(解析版) 题型:解答题
已知函数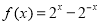 ,数列
,数列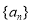 满足
满足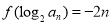 .
.
(1)求数列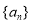 的通项公式;
的通项公式;
(2)证明:数列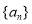 是递减数列.
是递减数列.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | 81 | C. | 243 | D. | 729 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com