
【题目】已知![]() ,命题
,命题![]() :对
:对![]() ,不等式
,不等式![]() 恒成立;命题
恒成立;命题![]() ,使得
,使得![]() 成立.
成立.
(1)若![]() 为真命题,求
为真命题,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,若
时,若![]() 假,
假, ![]() 为真,求
为真,求![]() 的取值范围.
的取值范围.
【答案】(1) 1≤m≤2.(2) (﹣∞,1)∪(1,2].
【解析】试题分析:本题主要考查简易逻辑,恒成立问题,不等式的解法.(1)由题意得出![]() ,然后解不等式即可.(2)由题意得出
,然后解不等式即可.(2)由题意得出![]() ,再根据p且q为假,p或q为真,得出p与q必然一真一假,即可解答.
,再根据p且q为假,p或q为真,得出p与q必然一真一假,即可解答.
试题解析:
(1)设![]() ,则
,则![]() 在[0,1]上单调递增,
在[0,1]上单调递增,
∴![]() .
.
∵对任意x∈[0,1],不等式2x﹣2≥m2﹣3m恒成立,
∴![]() ,即
,即![]() ,
,
解得1≤m≤2.
∴![]() 的取值范围为
的取值范围为![]() .
.
(2)a=1时, ![]() 区间[﹣1,1]上单调递增,
区间[﹣1,1]上单调递增,
∴![]() .
.
∵存在x∈[﹣1,1],使得m≤ax成立,
∴m≤1.
∵![]() 假,
假, ![]() 为真,
为真,
∴p与q一真一假,
①当p真q假时,
可得![]() ,解得1<m≤2;
,解得1<m≤2;
②当p假q真时,
可得![]() ,解得
,解得![]() .
.
综上可得1<m≤2或m<1.
∴实数m的取值范围是(﹣∞,1)∪(1,2].


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过3S微克/立方米,
的年平均浓度不得超过3S微克/立方米, ![]() 的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天
的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天![]() 的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
组别 |
| 频数(天) | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
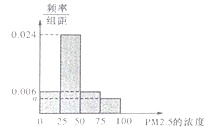
(Ⅰ)将这20天的测量结果按表中分组方法绘制成的样本频率分布直方图如图.
(ⅰ)求图中![]() 的值;
的值;
(ⅱ)在频率分布直方图中估算样本平均数,并根据样本估计总体的思想,从![]() 的年平均度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
的年平均度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
(Ⅱ)将频率视为概率,对于2016年的某3天,记这3天中该居民区![]() 的24小时平均浓度符合环境空气质量标准的天数为
的24小时平均浓度符合环境空气质量标准的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,将木兰溪流经市区河段分成![]() 段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如下表:
段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如下表:
南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
(Ⅰ)记评分在![]() 以上(包括
以上(包括![]() )为优良,从中任取一段,求在同一段中两岸环保评分均为优良的概率;
)为优良,从中任取一段,求在同一段中两岸环保评分均为优良的概率;
(Ⅱ)根据表中数据完成下面茎叶图;
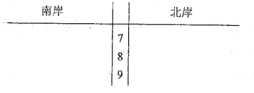
(Ⅲ)分别估计两岸分值的中位数,并计算它们的平均值,试从计算结果分析两岸环保情况,哪边保护更好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆G: ![]() 的离心率为
的离心率为![]() ,过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限).
,过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限).
(Ⅰ)求椭圆G的方程;
(Ⅱ)已知A为椭圆G的左顶点,平行于AM的直线l与椭圆G相交于B,C两点,请判断直线MB,MC是否关于直线m对称,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线E: ![]() (a>0,b>0)的渐近线方程为3x±4y=0,且过焦点垂直x轴的直线与双曲线E相交弦长为
(a>0,b>0)的渐近线方程为3x±4y=0,且过焦点垂直x轴的直线与双曲线E相交弦长为![]() ,过双曲线E中心的直线与双曲线E交于A,B两点,在双曲线E上取一点C(与A,B不重合),直线AC,BC 的斜率分别为k1,k2,则k1k2等于( )
,过双曲线E中心的直线与双曲线E交于A,B两点,在双曲线E上取一点C(与A,B不重合),直线AC,BC 的斜率分别为k1,k2,则k1k2等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com