
在直角坐标系xOy中,以O为圆心的圆与直线x-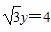 相切.
相切.
(1)求圆O的方程;
(2)圆O与x轴相交于A,B两点,圆内的动点P使|PA|,|PO|,|PB|成等比数列,求 ·
·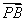 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
幂函数y=x-1及直线y=x、y=1、x=1将平面直角坐标系的第一象限分成八个“区域”:①、②、③、④、⑤、⑥、⑦、⑧(如图所示),那么幂函数y=x 的图象经过的“区域”是( )
的图象经过的“区域”是( )
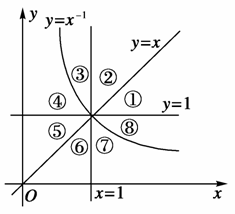
A.⑧,③ B.⑦,③
C.⑥,② D.⑤,①
查看答案和解析>>
科目:高中数学 来源: 题型:
定义在R上的函数f(x)满足f(x)+f(x+5)=16,当x∈(-1,4]时,f(x)=x2-2x,则函数f(x)在[0,2013]上的零点个数是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)的图象是连续不断的,有如下的x、f(x)对应值表:
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 123.56 | 21.45 | -7.82 | 11.57 | -53.76 | -126.49 |
函数f(x)在区间[1,6]上的零点有( )
A.2个 B.3个
C.至多2个 D.至少3个
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆C关于y轴对称,经过点(1,0)且被x轴分成两段弧长比为1∶2,则圆C的方程为 ( )
A. 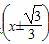 2+y2=
2+y2=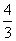 B.
B. 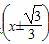 2+y2=
2+y2=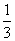
C.x2+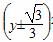 2=
2=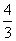 D.x2+
D.x2+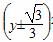 2=
2=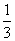
查看答案和解析>>
科目:高中数学 来源: 题型:
已知:圆C:x2+y2-8y+12=0,直线l:ax+y+2a=0.
(1)当a为何值时,直线l与圆C相切;
(2)当直线l与圆C相交于A,B两点,且|AB|=2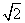 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
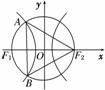
如图所示,F1,F2是双曲线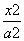 -
-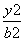 =1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点分别为A,B,且△F2AB是等边三角形,则双曲线的离心率为( )
=1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点分别为A,B,且△F2AB是等边三角形,则双曲线的离心率为( )
A.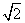 +1 B.
+1 B.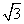 +1 C.
+1 C. 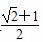 D.
D. 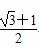
查看答案和解析>>
科目:高中数学 来源: 题型:
由①y=2x+5是一次函数;②y=2x+5的图像是一条直线;③一次函数的图像是一条直线.写一个“三段论”形式的正确推理,则作为大前提、小前提和结论的分别是( )
A.②①③ B.③①②
C.①②③ D.②③①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com