
分析 (Ⅰ)若k=1,联立直线和椭圆方程,结合相交弦的弦长公式以及|AB|=$\frac{\sqrt{10}}{2}$,即可求实数a的值;
(Ⅱ)根据$\overrightarrow{AC}$=2$\overrightarrow{CB}$关系,结合一元二次方程根与系数之间的关系,以及基本不等式进行求解即可.
解答 解:设A(x1,y1),B(x2,y2),
(Ⅰ)由$\left\{\begin{array}{l}{y=x+1}\\{3{x}^{2}+{y}^{2}=a}\end{array}\right.$得4x2+2x+1-a=0,
则x1+x2=$-\frac{1}{2}$,x1x2=$\frac{1-a}{4}$,
则|AB|=$\sqrt{2}|{x}_{1}-{x}_{2}|$=$\sqrt{2}•\sqrt{a-\frac{3}{4}}=\frac{\sqrt{10}}{2}$,解得a=2.
(Ⅱ)由$\left\{\begin{array}{l}{y=kx+1}\\{3{x}^{2}+{y}^{2}=a}\end{array}\right.$,得(3+k2)x2+2kx+1-a=0,
则x1+x2=-$\frac{2k}{3+{k}^{2}}$,x1x2=$\frac{1-a}{3+{k}^{2}}$,
由$\overrightarrow{AC}$=2$\overrightarrow{CB}$得(-x1,1-y1)=2(x2,y2-1),
解得x1=-2x2,代入上式得:
x1+x2=-x2=-$\frac{2k}{3+{k}^{2}}$,则x2=$\frac{2k}{3+{k}^{2}}$,
${S}_{△AOB}=\frac{1}{2}|OC|•|{x}_{1}-{x}_{2}|$=$\frac{3}{2}|{x}_{2}|=\frac{3|k|}{3+{k}^{2}}$=$\frac{3}{\frac{3}{|k|}+|k|}$$≤\frac{3}{2\sqrt{3}}=\frac{\sqrt{3}}{2}$,
当且仅当k2=3时取等号,此时x2=$\frac{2k}{3+{k}^{2}}$,x1x2=-2x22=-2×$\frac{4{k}^{2}}{(3+{k}^{2})^{2}}=-\frac{2}{3}$,
又x1x2=$\frac{1-a}{3+{k}^{2}}$=$\frac{1-a}{6}$,
则$\frac{1-a}{6}$=-$\frac{2}{3}$,解得a=5.
所以,△AOB面积的最大值为$\frac{\sqrt{3}}{2}$,此时椭圆的方程为3x2+y2=5.
点评 本题主要考查椭圆方程的求解,利用直线方程和椭圆方程构造方程组,转化为根与系数之间的关系是解决本题的关键.


科目:高中数学 来源: 题型:解答题
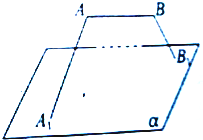 线段AB与平面α平行,α的斜线A1A、B1B与α所成的角分别为30°和60°,且∠A1AB=∠B1BA=90°,AB=2,A1B1=4,求AB与平面α的距离.
线段AB与平面α平行,α的斜线A1A、B1B与α所成的角分别为30°和60°,且∠A1AB=∠B1BA=90°,AB=2,A1B1=4,求AB与平面α的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知平行四边形ABCD与直角梯形ABEF所在的平面互相垂直,且AB=BE=$\frac{1}{2}$AF=1,BE∥AF,AB⊥AF,∠CBA=$\frac{π}{4}$,BC=$\sqrt{2}$,P为DF的中点.
如图,已知平行四边形ABCD与直角梯形ABEF所在的平面互相垂直,且AB=BE=$\frac{1}{2}$AF=1,BE∥AF,AB⊥AF,∠CBA=$\frac{π}{4}$,BC=$\sqrt{2}$,P为DF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
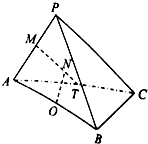 如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点.
如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com