
分析 f(x)的周期为2×(3-1)=4,解出ω,由f′($\frac{3}{2}$)<0得出f(1)=fmax(x)=1,利用正弦函数的性质解出φ,得到f(x)的解析式,再计算f($\frac{1}{3}$).
解答 解:∵x=1,x=3是函数f(x)=sin(ωx+φ)(ω>0)两个相邻的两个极值点,
∴f(x)的周期T=$\frac{2π}{ω}$=2×(3-1)=4,∴ω=$\frac{π}{2}$.
∵f′($\frac{3}{2}$)<0,
∴f(x)在[1,3]上是减函数,∴f(1)=sin($\frac{π}{2}$+φ)=1,
∴$\frac{π}{2}$+φ=$\frac{π}{2}+2kπ$,∴φ=2kπ.
∴f($\frac{1}{3}$)=sin($\frac{π}{6}+2kπ$)=sin$\frac{π}{6}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了正弦函数的图象与性质,导数与函数单调性的关系,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
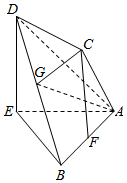 如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC、BD,G为BD的中点,AB=AC=AE=BE=2.
如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC、BD,G为BD的中点,AB=AC=AE=BE=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com