
| F1B |
| 3 |
| OB |
| OH |
| AB |
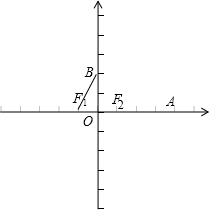 解:(Ⅰ)由题意知,F1(-1,0),F2(1,0);
解:(Ⅰ)由题意知,F1(-1,0),F2(1,0);| F1B |
| c |
| a |
| OB |
| F1B |
| 3 |
| OB |
| c |
| a |
| 3 |
| 3 |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| 2 |
| 16k |
| 4k2+3 |
| 16k |
| 4k2+3 |
| -8k2+6 |
| 4k2+3 |
| 8k |
| 4k2+3 |
| -4k2+3 |
| 4k2+3 |
| OH |
| AB |
| -4k2+3 |
| -8k |
| ||
| 0-2 |
| ||||
| 2 |


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
 某校开设有数学史选修课,为了解学生对数学史的掌握情况,举办了数学史趣味知识竞赛,现将成绩统计如下.请你根据尚未完成任务的频率分布表和局部污损的频率分布直方图,解答下列问题:
某校开设有数学史选修课,为了解学生对数学史的掌握情况,举办了数学史趣味知识竞赛,现将成绩统计如下.请你根据尚未完成任务的频率分布表和局部污损的频率分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| [50,60) | 2 | |
| [60,70) | 7 | |
| [70,80) | 10 | |
| [80,90) | x | |
| [90,100] | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
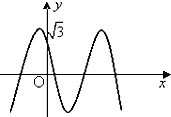 如图,函数f(x)=2cos(ωx+θ)(x∈R,ω>0,0≤θ≤
如图,函数f(x)=2cos(ωx+θ)(x∈R,ω>0,0≤θ≤| π |
| 2 |
| 3 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 12 |
| 8 |
| 5 |
| sinx+sin2x |
| 1+cosx+cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是8的平行四边形MNEF.
如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是8的平行四边形MNEF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com