
分析 (Ⅰ)由|x-a|<b解得{x|a-b<x<a+b},结合不等式|x-a|<b的解集为{x|2<x<4},可得a-b=2且a+b=4,由此求得a、b的值.
(Ⅱ)由条件利用柯西不等式求得x,y,z的最大值和最小值.
解答 解:(Ⅰ)由|x-a|<b解得{x|a-b<x<a+b},结合不等式|x-a|<b的解集为{x|2<x<4},
可得a-b=2且a+b=4,解得a=3,b=1.
(Ⅱ)依题意有 $\frac{{(x-1)}^{2}}{16}$+$\frac{{(y+2)}^{2}}{5}$+$\frac{{(z-3)}^{2}}{4}$=1,由柯西不等式知
[42+${(\sqrt{5})}^{2}$+22]•[$\frac{{(x-1)}^{2}}{16}$+$\frac{{(y+2)}^{2}}{5}$+$\frac{{(z-3)}^{2}}{4}$]≥${[4•\frac{x-1}{4}+\sqrt{5}•\frac{y+2}{\sqrt{5}}+2•\frac{z-3}{2}]}^{2}$,
即25×1≥(x+y+z-2)2,解得-3≤x+y+z≤7,
当且仅当x=$\frac{21}{5}$,y=-1,z=$\frac{19}{5}$时,x+y+z=7;
当且仅当x=-$\frac{11}{5}$,y=-3,z=$\frac{11}{5}$时,x+y+z=-3;
所以,x+y+z的最大值为7,最小值为-3.
点评 本题主要考查绝对值不等式的解法,柯西不等式的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{5}+\frac{3}{5}i$ | B. | $-\frac{3}{5}+\frac{4}{5}i$ | C. | $-\frac{1}{2}+\frac{3}{2}i$ | D. | $-\frac{1}{2}-\frac{3}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
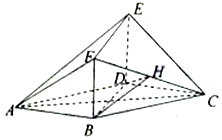 如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.
如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -3 | C. | -$\frac{7}{5}$ | D. | -$\frac{11}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,6) | B. | (-1,6) | C. | (-2,1) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 安全感指数 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100] |
| 男居民人数 | 8 | 16 | 226 | 131 | 119 |
| 女居民人数 | 12 | 14 | 174 | 122 | 178 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com