
分析 根据题意,设M(x0,y0),分析可得P的坐标,分析可得$x_0^2+{(2{y_0})^2}=1$,整理得$\frac{x_0^2}{4}+y_0^2=1$,即可得M的轨迹是椭圆,由椭圆的标准方程分析可得其焦点坐标以及离心率.
解答 解:根据题意,设M(x0,y0),又由线段PD的中点M,则P(x0,2y0),
点P在圆上运动,所以$x_0^2+{(2{y_0})^2}=1$,整理得$\frac{x_0^2}{4}+y_0^2=1$,
所以点M的轨迹是椭圆,
该椭圆的焦点是$({±\sqrt{3},0})$,离心率为$\frac{{\sqrt{3}}}{2}$.
点评 本题考查曲线的轨迹方程,涉及椭圆的几何性质,关键是求出轨迹的方程.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,某中学兴趣小组设计的自动小车按下面程序运行:
如图所示,某中学兴趣小组设计的自动小车按下面程序运行:查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\{k\left|{k>\frac{{\sqrt{6}}}{3}}\right.或k<-\frac{{\sqrt{6}}}{3}\}$ | B. | $\{k\left|{-\frac{{\sqrt{6}}}{3}<k<\frac{{\sqrt{6}}}{3}}\right.\}$ | C. | $\{k\left|{k≥\frac{{\sqrt{6}}}{3}}\right.或k≤-\frac{{\sqrt{6}}}{3}\}$ | D. | $\{k\left|{-\frac{{\sqrt{6}}}{3}≤k≤\frac{{\sqrt{6}}}{3}}\right.\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥O-ABC中,AO⊥平面OBC,且OA=OB=OC=2,∠BOC=60°,点E,F分别是AB,AC的中点,H为EF的中点,过EF的动平面与线段OA交于点A1,与线段OB,OC的延长线分别相交于点B1,C1.
如图,三棱锥O-ABC中,AO⊥平面OBC,且OA=OB=OC=2,∠BOC=60°,点E,F分别是AB,AC的中点,H为EF的中点,过EF的动平面与线段OA交于点A1,与线段OB,OC的延长线分别相交于点B1,C1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
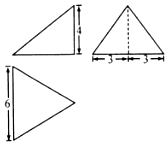 如图,某三棱锥的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和等边三角形,若该三棱锥的顶点都在同一球面上,则该球的表面积为( )
如图,某三棱锥的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和等边三角形,若该三棱锥的顶点都在同一球面上,则该球的表面积为( )| A. | 27π | B. | 48π | C. | 64π | D. | 81π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a>b>c | C. | b<a<c | D. | b>a>c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com