
 如图所示,某中学兴趣小组设计的自动小车按下面程序运行:
如图所示,某中学兴趣小组设计的自动小车按下面程序运行:分析 (1)由题意得出向下的概率和向右概率,从A过M到B,有两次向下,再有一次向下与一次向右组合,求得概率值,同理可求海宝过点从A经过N到点C的概率;
(2)求出X=1,2,3时相应的概率,从而可求随机变量X的分布列及期望.
解答 解:(1)由题意,向下概率为$\frac{1}{3}$,则向右概率为1-$\frac{1}{3}$=$\frac{2}{3}$;
从A过M到B,先有两次向下,再有一次向下与一次向右组合,
其概率为${(\frac{1}{3})}^{2}$•${C}_{2}^{1}$•$\frac{1}{3}$•$\frac{2}{3}$=$\frac{4}{81}$;
从A过N到C,概率为${C}_{2}^{1}$•$\frac{1}{3}$•$\frac{2}{3}$•${C}_{2}^{1}$•$\frac{1}{3}$•$\frac{2}{3}$=$\frac{16}{81}$;
(2)P(X=1)=($\frac{1}{3}$)3+${C}_{3}^{2}$•($\frac{1}{3}$)2•$\frac{2}{3}$•$\frac{1}{3}$=$\frac{3}{27}$;
P(X=2)=${C}_{4}^{2}$•($\frac{1}{3}$)2•($\frac{2}{3}$)2=$\frac{8}{27}$;
P(X=3)=($\frac{2}{3}$)3+${C}_{3}^{2}$•($\frac{2}{3}$)2•$\frac{1}{3}$•$\frac{2}{3}$=$\frac{16}{27}$,
∴X的分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{3}{27}$ | $\frac{8}{27}$ | $\frac{16}{27}$ |
点评 本题考查了等可能事件的概率以及离散型随机变量的分布列和数学期望,是中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 8 | D. | -8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $3-\sqrt{3}$ | D. | $3+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
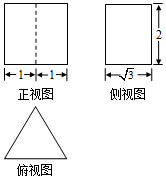
| A. | 12 | B. | 8+2$\sqrt{3}$ | C. | 12+2$\sqrt{3}$ | D. | 12+4$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com