Question

2．已知集合A={（x，y）||x|+|y|=a，a＞0}，B={（x，y）||xy|+1=|x|+|y|}．若A∩B是平面上正八边形的顶点所构成的集合，则a的值为$\sqrt{2}$或2+$\sqrt{2}$．

Answer 1

分析 根据曲线性质求出集合A，B对应的图象，结合两角和差的正切公式进行求解即可．

解答 解：A={（x，y）||x|+|y|=a，a＞0}，
x≥0，y≥0时，即x+y=a表示在第一象限内的线段
将x，y分别换成-x，-y方程不变，因此
|x|+|y|=a关于x轴对称，也关于y轴对称
那么，集合A={（x，y）||x|+|y|=a，a＞0}
表示点集为正方形，
∵|xy|+1=|x|+|y|
∴|xy|-|x|-|y|+1=0
即（|x|-1）（|y|-1）=0
∴|x|=1或|y|=1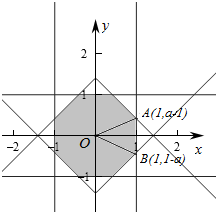
即x=±1，y=±1
B={（x，y）|x=±1，或x=±1}，表示2组平行线，
A∩B为8个点，构成正八边形
①如图1，∠AOB=45°
又A（1，a-1）
∴tan∠xOA=a-1
tan∠AOB=tan2∠xOA=$\frac{2tan∠xOA}{1-ta{n}^{2}∠xOA}$=$\frac{2（a-1）}{1-（a-1）^{2}}=\frac{2a-2}{2a-{a}^{2}}$=1，
即2a-2=2a-a²，
∴a²=2
∵a＞0，∴a=$\sqrt{2}$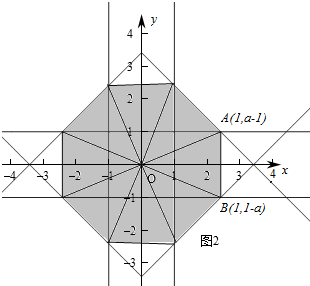
②如图2，∠AOB=45°
又A（a-1，1）
∴tan∠xOA=$\frac{1}{a-1}$，
tan∠AOB=tan2∠xOA=$\frac{2tan∠xOA}{1-ta{n}^{2}∠xOA}$=$\frac{\frac{2}{a-1}}{1-（\frac{1}{a-1}）^{2}}$=$\frac{2（a-1）}{（a-1）^{2}-1}$=1，
即2a-2=-2a+a²，
∴a²-4a+2=0，
解得a=2+$\sqrt{2}$或a=2-$\sqrt{2}$（舍），
综上a=$\sqrt{2}$或a=2+$\sqrt{2}$，
故答案为：$\sqrt{2}$或2+$\sqrt{2}$

点评 本题主要考查集合的基本运算，利用曲线的轨迹，结合两角和差的正切公式是解决本题的关键．综合性较强，难度较大．