
设函数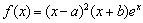 ,a、b
,a、b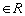 ,x=a是
,x=a是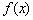 的一个极大值点.
的一个极大值点.
(1)若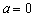 ,求b的取值范围;
,求b的取值范围;
(2)当a是给定的实常数,设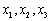 是
是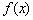 的3个极值点,问是否存在实数b,可找到
的3个极值点,问是否存在实数b,可找到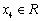 ,使得
,使得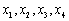 的某种排列
的某种排列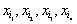 (其中
(其中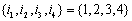 )依次成等差数列?若存在,求所有的b及相应的
)依次成等差数列?若存在,求所有的b及相应的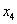 ;若不存在,请说明理由.
;若不存在,请说明理由.
解析:(1)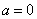 时,
时,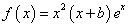 ,
,
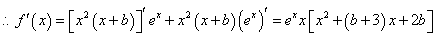 ,……1分
,……1分
令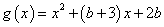 ,
,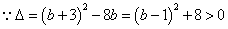 ,
,
可设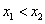 是
是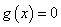 的两个根,……………………………………2分
的两个根,……………………………………2分
①当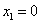 或
或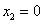 时,则
时,则 不是极值点,不合题意;
不是极值点,不合题意;
②当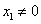 且
且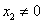 时,由于
时,由于 是
是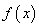 的极大值点,
的极大值点,
故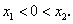
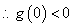 ,即
,即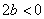 ,
,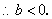 故b的取值范围是
故b的取值范围是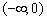 . ……5分
. ……5分
(2)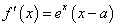
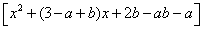 ,
,
令 ,
,
则 ,于是,假设
,于是,假设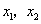 是
是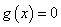 的两个实根,且
的两个实根,且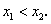
由(1)可知,必有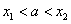 ,且
,且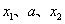 是
是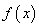 的三个极值点,
的三个极值点,
则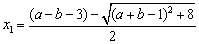 ,
,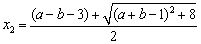 . ……6分
. ……6分
假设存在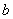 及
及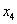 满足题意,不妨只考虑公差大于零的情形,即:
满足题意,不妨只考虑公差大于零的情形,即:
①当排列为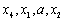 或
或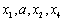 ,则
,则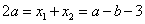 ,即
,即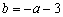 时,[]
时,[]
于是 或
或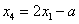
即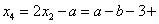
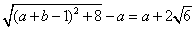
或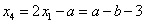
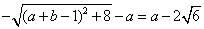 ……………………8分
……………………8分
②当排列为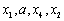 或
或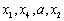 ,则
,则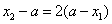 或
或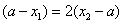
(i)若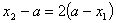 ,于是
,于是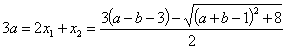 ,
,
即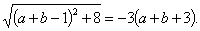 两边平方得
两边平方得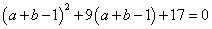 ,
,
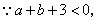 于是
于是
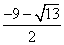 ,从而
,从而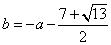 ,
,
此时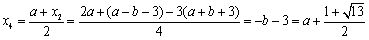 ………10分
………10分
(ii)若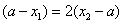 ,于是
,于是 ,
,
即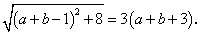 两边平方得
两边平方得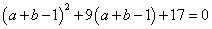 ,
,
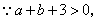 于是
于是
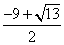 ,从而
,从而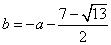
此时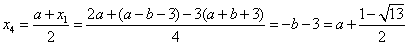
综上所述,存在b满足题意,当b=-a-3时,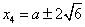 ;当
;当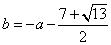 时,
时,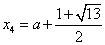 ;
;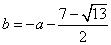 时,
时,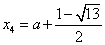 .
.


科目:高中数学 来源: 题型:
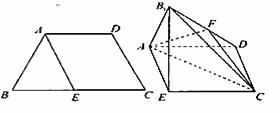
)已知四边形ABCD满足AD∥BC,BA=AD=DC=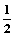 BC=a,E是BC的中点,将△BAE沿AE折起到
BC=a,E是BC的中点,将△BAE沿AE折起到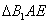 的位置,使平面
的位置,使平面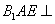 平面
平面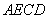 ,F为B1D的中点.
,F为B1D的中点.
(Ⅰ)证明:B1E∥平面ACF;
(Ⅱ)求平面ADB1与平面ECB1所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,SA⊥平面ABC,AB ⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.
⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.
求证:AF⊥SC.
证明:要证AF⊥SC,只需证SC⊥平 面AEF,只需证AE⊥SC(因为______),只需证______,只需证AE
面AEF,只需证AE⊥SC(因为______),只需证______,只需证AE ⊥BC(因为________),只需证BC⊥平面SAB,只
⊥BC(因为________),只需证BC⊥平面SAB,只 需证BC⊥SA(因为______).由SA⊥平面ABC可知,上式成立.
需证BC⊥SA(因为______).由SA⊥平面ABC可知,上式成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
有下列叙述:
①“a>b” 的反面是“a<b”;
的反面是“a<b”;
②“x=y”的反面是“x>y或x<y”;
③“三角形的外心在三角形外”的反面是“三角形的外心在三角形内”;
④“三角形最多有一个钝角”的反面是“三角形没有钝角”.
其中正确的叙述有________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com