
【题目】设数列![]() 为首项是4,公差为1的等差数列,
为首项是4,公差为1的等差数列,![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() 。
。
(1)求数列![]() 及
及![]() 的通项公式
的通项公式![]() 和
和![]() ;
;
(2)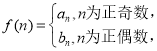 问是否存在
问是否存在![]() 使
使![]() 成立?若存在,求出
成立?若存在,求出![]() ,若不存在,说明理由;
,若不存在,说明理由;
(3)对任意的正数![]() ,不等式
,不等式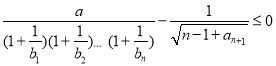 恒成立,求正数
恒成立,求正数![]() 的取值范围。
的取值范围。
【答案】(1)![]() ;(2)不存在,理由见解析;(3)
;(2)不存在,理由见解析;(3)
【解析】
(1)根据等差数列通项公式求得![]() 的通项公式,利用
的通项公式,利用 求得
求得![]() 的通项公式.
的通项公式.
(2)假设存在符合条件的![]() ,对
,对![]() 分为奇数和偶数两种情况进行分类讨论,结合
分为奇数和偶数两种情况进行分类讨论,结合![]() ,判断出符合条件的正整数
,判断出符合条件的正整数![]() 不存在.
不存在.
(3)将原不等式分离常数![]() ,利用数列的单调性求得
,利用数列的单调性求得![]() 的取值范围.
的取值范围.
(1)依题意数列![]() 为首项是
为首项是![]() ,公差为
,公差为![]() 的等差数列,所以
的等差数列,所以![]() .由于
.由于![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() .当
.当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() ,
,![]() 也符合上式,故
也符合上式,故![]() .
.
(2)假设符合条件的![]() 存在.由(1)得
存在.由(1)得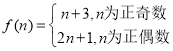 .
.
当![]() 为正奇数时,
为正奇数时,![]() 为正偶数,由
为正偶数,由![]() 得
得![]() ,解得
,解得![]() ,不符合题意.
,不符合题意.
当![]() 为正偶数时,
为正偶数时,![]() 为正奇数,由
为正奇数,由![]() 得
得![]() ,解得
,解得![]() ,不符合题意.
,不符合题意.
综上所述,符合条件的正整数![]() 不存在.
不存在.
(3)由(1)知![]() ,代入得
,代入得![]() .
.
设![]() ,则
,则
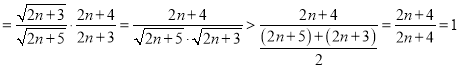 ,即
,即![]() ,所以
,所以![]() 是单调递增数列,最小值为
是单调递增数列,最小值为![]() .所以
.所以![]() 的取值范围是
的取值范围是 .
.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与圆
与圆![]() 相切,圆心
相切,圆心![]() 的坐标为
的坐标为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 没有公共点,求
没有公共点,求![]() 的取值范围;
的取值范围;
(3)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是奇函数(其中
是奇函数(其中![]() )
)
(1)求实数m的值;
(2)已知关于x的方程![]() 在区间
在区间![]() 上有实数解,求实数k的取值范围;
上有实数解,求实数k的取值范围;
(3)当![]() 时,
时,![]() 的值域是
的值域是![]() ,求实数n与a的值.
,求实数n与a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某油库的设计容量为30万吨,年初储量为10万吨,从年初起计划每月购进石油![]() 万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前
万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前![]() 个月的需求量
个月的需求量![]() (万吨)与
(万吨)与![]() 的函数关系为
的函数关系为![]() ,并且前4个月区域外的需求量为20万吨.
,并且前4个月区域外的需求量为20万吨.
(1)试写出第![]() 个月石油调出后,油库内储油量
个月石油调出后,油库内储油量![]() (万吨)与
(万吨)与![]() 的函数关系式;
的函数关系式;
(2)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超出油库的容量,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记无穷数列![]() 的前
的前![]() 项中最大值为
项中最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]() ,
,![]() .
.
(1)若![]() ,请写出
,请写出![]() 的值;
的值;
(2)求证:“数列![]() 是等差数列”是“数列
是等差数列”是“数列![]() 是等差数列”的充要条件;
是等差数列”的充要条件;
(3)若对任意![]() ,有
,有![]() ,且
,且![]() ,请问:是否存在
,请问:是否存在![]() ,使得对于任意不小于
,使得对于任意不小于![]() 的正整数
的正整数![]() ,有
,有![]() 成立?请说明理由.
成立?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,长轴长为
,长轴长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程及离心率;
的标准方程及离心率;
(Ⅱ)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,求证:由点
,求证:由点![]() 构成的曲线
构成的曲线![]() 关于直线
关于直线![]() 对称.
对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax3+3x2+3x(a≠0).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在区间(1,2)是增函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
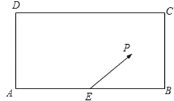
【题目】某校兴趣小组在如图所示的矩形区域![]() 内举行机器人拦截挑战赛,在
内举行机器人拦截挑战赛,在![]() 处按
处按![]() 方向释放机器人甲,同时在
方向释放机器人甲,同时在![]() 处按某方向释放机器人乙,设机器人乙在
处按某方向释放机器人乙,设机器人乙在![]() 处成功拦截机器人甲.若点
处成功拦截机器人甲.若点![]() 在矩形区域
在矩形区域![]() 内(包含边界),则挑战成功,否则挑战失败.已知
内(包含边界),则挑战成功,否则挑战失败.已知![]() 米,
米,![]() 为
为![]() 中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线运动方式行进,记
中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线运动方式行进,记![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(1)若![]() ,
,![]() 足够长,则如何设置机器人乙的释放角度才能挑战成功?(结果精确到
足够长,则如何设置机器人乙的释放角度才能挑战成功?(结果精确到![]() );
);
(2)如何设计矩形区域![]() 的宽
的宽![]() 的长度,才能确保无论
的长度,才能确保无论![]() 的值为多少,总可以通过设置机器人乙的释放角度使机器人乙在矩形区域
的值为多少,总可以通过设置机器人乙的释放角度使机器人乙在矩形区域![]() 内成功拦截机器人甲?
内成功拦截机器人甲?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com