
���� ��1����$\left\{\begin{array}{l}x=cos��\\ y=sin��\end{array}\right.$��x2+y2=1�����ü�������ֱ�����껥�������õ�ֱ��l��ֱ�����귽�̣�
��2�����ò��������Բ�ĵ�ֱ�ߵľ��룬���ɵó����ۣ�
��� �⣺��1����$\left\{\begin{array}{l}x=cos��\\ y=sin��\end{array}\right.$��x2+y2=1��
�ɦѣ�2cos��-sin�ȣ�=6����2��cos��+��sin��=6��
ֱ�ߵ�ֱ�����귽��Ϊ��2x+y-6=0��
��2��Բ��Ϊ��0��0����r=1��Բ�ĵ�ֱ�ߵľ���$d=\frac{{|{2cos��+sin��-6}|}}{{\sqrt{{2^2}+{1^2}}}}=\frac{{|{\sqrt{5}sin����+�գ�-6}|}}{{\sqrt{5}}}��sin��=\frac{{2\sqrt{5}}}{5}��cos��=\frac{{\sqrt{5}}}{5}$��
��$��+��=\frac{��}{2}$ʱP��ֱ�ߵľ�����̣���ʱ$x=cos��=sin��=\frac{{2\sqrt{5}}}{5}��y=sin��=co��=\frac{{\sqrt{5}}}{5}$��
���Ե�P������$��\frac{{2\sqrt{5}}}{5}��\frac{{\sqrt{5}}}{5}��$��
Բ�ϵĵ�P��ֱ�ߵ���̾���Ϊ$\frac{{6\sqrt{5}}}{5}-1$��������Ϊ$\frac{{6\sqrt{5}}}{5}+1$��
���� ���⿼��������̣������귽����ֱ�����귽�̵Ļ���������㵽ֱ�ߵľ��빫ʽ�������е��⣮


 С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д� ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1��2} | B�� | {1}��∅ | C�� | $\left\{{1��\sqrt{2}��2}\right\}$ | D�� | {1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��-\frac{1}{3}��-\frac{1}{4}��$��$��\frac{1}{2}��1��$ | B�� | $��-\frac{1}{2}��-\frac{1}{3}��$��$��\frac{1}{3}��\frac{1}{2}��$ | C�� | $��-\frac{1}{2}��-\frac{1}{3}��$��$��\frac{1}{2}��1��$ | D�� | $��-\frac{1}{3}��-\frac{1}{4}��$��$��\frac{1}{3}��\frac{1}{2}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20 | B�� | 36 | C�� | 48 | D�� | 52 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
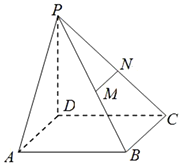 ��ͼ����֪����P-ABCD�У�PD�͵���ABCD���ҵ���ABCD�DZ߳�Ϊ2�������Σ�M��N�ֱ�ΪPB��PC���е㣮
��ͼ����֪����P-ABCD�У�PD�͵���ABCD���ҵ���ABCD�DZ߳�Ϊ2�������Σ�M��N�ֱ�ΪPB��PC���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com