
(本题满分14分)已知圆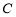 :
: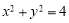 .
.
(Ⅰ)直线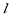 过点
过点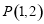 ,且与圆
,且与圆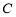 交于
交于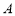 、
、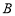 两点,若
两点,若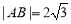 ,求直线
,求直线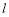 的方程;
的方程;
(Ⅱ)过圆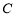 上一动点
上一动点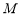 作平行于
作平行于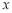 轴的直线
轴的直线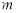 ,设
,设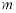 与
与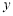 轴的交点为
轴的交点为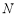 ,若向量
,若向量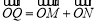 ,求动点
,求动点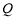 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
(Ⅰ)x=1,3x-4y+5=0,;(Ⅱ) (y≠0)轨迹为长轴长为8,短轴长为4,焦距为4
(y≠0)轨迹为长轴长为8,短轴长为4,焦距为4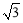 且焦点在y轴上的椭圆且去掉椭圆短轴的两个端点
且焦点在y轴上的椭圆且去掉椭圆短轴的两个端点
【解析】
试题分析:(Ⅰ)由直线与圆位置关系得:半径,半弦长,圆心到直线距离构成勾股,即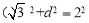 ,因此d=1,又直线
,因此d=1,又直线 过点
过点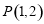 ,故利用直线方程点斜式求解,注意先讨论斜率不存在情况:若
,故利用直线方程点斜式求解,注意先讨论斜率不存在情况:若 ⊥x轴,直线方程为x=1,A(1,-
⊥x轴,直线方程为x=1,A(1,-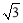 ),B(1,
),B(1,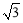 ),
), ,适合;若
,适合;若 的斜率存在,设
的斜率存在,设 的方程为y=k(x-1)+2,圆心到直线的距离为d=1=
的方程为y=k(x-1)+2,圆心到直线的距离为d=1=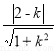 解得k=
解得k=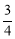 ,直线方程为3x-4y+5=0,(Ⅱ)相关点法求轨迹方程:先找出所求的与已知动点之间关系,代入已知动点轨迹,化简即得所求动点轨迹方程:设M(
,直线方程为3x-4y+5=0,(Ⅱ)相关点法求轨迹方程:先找出所求的与已知动点之间关系,代入已知动点轨迹,化简即得所求动点轨迹方程:设M( ,
, )(
)( ≠0).则N(0,
≠0).则N(0, ),Q(x,y),则
),Q(x,y),则  ,又
,又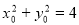 ,动点Q的轨迹方程为
,动点Q的轨迹方程为 (y≠0)轨迹为长轴长为8,短轴长为4,焦距为4
(y≠0)轨迹为长轴长为8,短轴长为4,焦距为4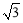 且焦点在y轴上的椭圆且去掉椭圆短轴的两个端点
且焦点在y轴上的椭圆且去掉椭圆短轴的两个端点
试题解析:【解析】
(Ⅰ)若 ⊥x轴,直线方程为x=1,A(1,-
⊥x轴,直线方程为x=1,A(1,-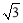 ),B(1,
),B(1,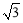 ),
), ,适合---3分
,适合---3分
若 的斜率存在,设
的斜率存在,设 的方程为y=k(x-1)+2,圆心到直线的距离为d=
的方程为y=k(x-1)+2,圆心到直线的距离为d=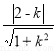 ,圆半径为2,故
,圆半径为2,故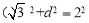 ,k=
,k=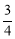 ,直线方程为3x-4y+5=0,
,直线方程为3x-4y+5=0,
综上所求直线 的方程为x=1,3x-4y+5=0,;
的方程为x=1,3x-4y+5=0,;
(Ⅱ)设M( ,
, )(
)( ≠0).则N(0,
≠0).则N(0, ),Q(x,y),则
),Q(x,y),则 
又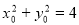 ,动点Q的轨迹方程为
,动点Q的轨迹方程为 (y≠0)
(y≠0)
轨迹为长轴长为8,短轴长为4,焦距为4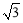 且焦点在y轴上的椭圆且去掉椭圆短轴的两个端点.----6分
且焦点在y轴上的椭圆且去掉椭圆短轴的两个端点.----6分
考点:直线与圆位置关系,轨迹方程


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014-2015学年江苏省等五校高三12月第一次联考理科数学试卷(解析版) 题型:解答题
(本题满分10分)已知数列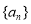 是等差数列,且
是等差数列,且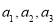 是
是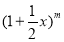 展开式的前三项的系数.
展开式的前三项的系数.
(1)求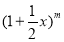 展开式的中间项;
展开式的中间项;
(2)当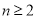 时,试比较
时,试比较 与
与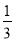 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2015届江苏教育学院附属高中高三上学期期中文科数学试卷(解析版) 题型:填空题
给出以下四个命题:
①已知命题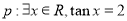 ;命题
;命题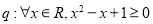 .则命题
.则命题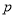 和
和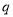 都是真命题;
都是真命题;
②过点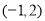 且在
且在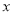 轴和
轴和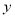 轴上的截距相等的直线方程是
轴上的截距相等的直线方程是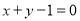 ;
;
③函数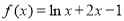 在定义域内有且只有一个零点;
在定义域内有且只有一个零点;
④先将函数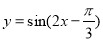 的图像向右平移
的图像向右平移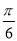 个单位,再将新函数的周期扩大为原来的两倍,则所得图像的函数解析式为
个单位,再将新函数的周期扩大为原来的两倍,则所得图像的函数解析式为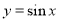 .
.
其中正确命题的序号为 .(把你认为正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源:2015届江苏教育学院附属高中高三上学期期中理科数学试卷(解析版) 题型:填空题
给出以下四个命题:
①已知命题 ;命题
;命题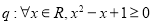 .则命题
.则命题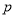 和
和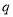 都是真命题;
都是真命题;
②过点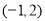 且在
且在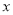 轴和
轴和 轴上的截距相等的直线方程是
轴上的截距相等的直线方程是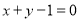 ;
;
③函数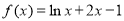 在定义域内有且只有一个零点;
在定义域内有且只有一个零点;
④先将函数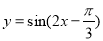 的图像向右平移
的图像向右平移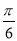 个单位,再将新函数的周期扩大为原来的两倍,则所得图像的函数解析式为
个单位,再将新函数的周期扩大为原来的两倍,则所得图像的函数解析式为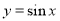 .
.
其中正确命题的序号为 .(把你认为正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省嘉兴市高三新高考单科综合调研三理科数学试卷(解析版) 题型:填空题
已知圆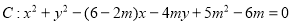 ,定直线
,定直线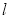 经过点
经过点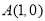 ,若对任意的实数
,若对任意的实数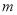 ,定直线
,定直线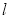 被圆
被圆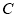 截得的弦长始终为定值
截得的弦长始终为定值 ,求得此定值
,求得此定值 等于 .
等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com