考点:函数的值域
专题:函数的性质及应用
分析:可知y=x2+2ax+1的图象开口向上,对称轴为x=-a,分类讨论可得.
解答:
解:y=x2+2ax+1的图象开口向上,对称轴为x=-a,
①当-a<0,即a>0时,y=x2+2ax+1在[0,2]上单调递增,
由二次函数可知ymin=1,ymax=5+4a,
∴函数的值域为[1,5+4a];
②当-a>2即a<-2时,函数在[0,2]上单调递减,
由二次函数可知ymin=5+4a,ymax=1,
∴函数的值域为[5+4a,1];
③当0≤-a≤1即-1≤a≤0时,y=x2+2ax+1在[0,-a]上单调递减,在[-a,2]上单调递增,
ymin=a2-2a×a+1=1-a2,ymax=5+4a,
此时函数的值域为[1-a2,5+4a];
④当1<-a≤2,即-2≤a<-1时,y=x2+2ax+1在[0,a]上单调递减,在[a,2]上单调递增,
ymin=a2-2a×a+1=1-a2,ymax=1,
此时函数的值域为[1-a2,1];
故答案为:当a>0时,函数的值域为[1,5+4a],
当a<-2时,函数的值域为[5+4a,1];
当-1≤a≤0时,函数的值域为[1-a2,5+4a];
当-2≤a<-1时,函数的值域为[1-a2,1].
点评:本题考查函数的值域,涉及分类讨论的思想,属中档题.



 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案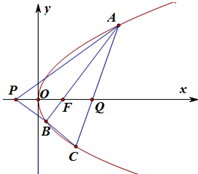 已知抛物线y2=4x的焦点F,过F作直线l交抛物线于A(xA,yA),B(xB,yB)两点,其中点A在x轴上方.
已知抛物线y2=4x的焦点F,过F作直线l交抛物线于A(xA,yA),B(xB,yB)两点,其中点A在x轴上方.