
分析 (Ⅰ)设A表示事件“抽取3张卡片上的数字之和大于或等于8”,任取三张卡片,利用列举法求出三张卡片上的数字全部可能的结果种数和数字之和大于或等于8的种数,由此能求出3张卡片上数字之和大于或等于8的概率.
(Ⅱ)设B表示事件“至少一次抽到3”,利用列举法能求出两次抽取的卡片中至少一次抽到数字3的概率.
解答 解:(Ⅰ)设A表示事件“抽取3张卡片上的数字之和大于或等于8”,
任取三张卡片,三张卡片上的数字全部可能的结果是
(1、2、3),(1、2、4),(1、3、4),(2、3、4),共4种,
数字之和大于或等于8的是(1、3、4),(2、3、4),共2种,
所以P(A)=$\frac{2}{4}=\frac{1}{2}$.…(6分)
(Ⅱ)设B表示事件“至少一次抽到3”,
第一次抽1张,放回后再抽取1张的全部可能结果为:
(1、1)(1、2)(1、3)(1、4)(2、1)(2、2)(2、3)(2、4)
(3、1)(3、2)(3、3)(3、4)(4、1)(4、2)(4、3)(4、4),共16个
事件B包含的结果有(1、3)(3、1)(2、3)(3、2)(3、3)(3、4)(4、3),共7个,
所以所求事件的概率为P(B)=$\frac{7}{16}$.…(12分)
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 60° | C. | 120° | D. | 135° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
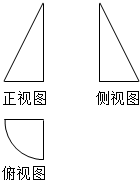 一个几何体的三视图如图所示,其中正视图与侧视图都是斜边长为2的直角三角形,俯视图是半径为1的$\frac{1}{4}$圆周和两条半径,则这个几何体的体积为( )
一个几何体的三视图如图所示,其中正视图与侧视图都是斜边长为2的直角三角形,俯视图是半径为1的$\frac{1}{4}$圆周和两条半径,则这个几何体的体积为( )| A. | $\frac{\sqrt{3}}{12}$π | B. | $\frac{\sqrt{3}}{6}$π | C. | $\frac{\sqrt{3}}{4}$π | D. | $\frac{\sqrt{3}}{3}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com