
| A. | ① | B. | ② | C. | ③ | D. | ④ |
分析 通过特殊值判断①②,通过通分判断③,通过基本不等式的性质判断④.
解答 解:如果a>b>0,且a+b=1,
那么①$\frac{a}{b}<1$,②$\frac{1}{b}<\frac{1}{a}$,令a=0.8,b=0.2,显然不成立,故①②错误;
③$\frac{1}{b}$+$\frac{1}{a}$=$\frac{a+b}{ab}$=$\frac{1}{ab}$,故$\frac{1}{b}+\frac{1}{a}<\frac{1}{ab}$错误;
④1=a+b>2$\sqrt{ab}$,故$ab<\frac{1}{4}$,
故④正确,
故选:D.
点评 本题考察了不等式的基本性质,特殊值法是常用简便的方法之一,本题是一道基础题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
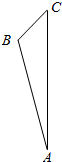 在△ABC中,∠BAC=10°,∠ACB=30°,将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1,则在所有旋转过程中,直线B1C与直线AC1所成角的取值范围为[10°,50°].
在△ABC中,∠BAC=10°,∠ACB=30°,将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1,则在所有旋转过程中,直线B1C与直线AC1所成角的取值范围为[10°,50°].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=b<c | B. | a<b<c | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com