
分析 (1)因为复数z所对应的点在一、三象限的角平分线上,可得m2+5m+6=m2-2m-15,解得m.
(2)当实数m=-1时,z=(1-5+6)+(1+2-15)i=2-12i.再利用复数的运算法则、模的计算公式即可得出.
解答 解:(1)因为复数z所对应的点在一、三象限的角平分线上,
所以m2+5m+6=m2-2m-15,…(4分)
解得m=-3.…(6分)
(2)当实数m=-1时,z=(1-5+6)+(1+2-15)i=2-12i.…(10分)
∴$|{\frac{z}{1+i}}|=|{\frac{2-12i}{1+i}}|=\frac{{|{2-12i}|}}{{|{1+i}|}}=\frac{{\sqrt{148}}}{{\sqrt{2}}}=\sqrt{74}$,
所以$|{\frac{z}{1+i}}|$的值为$\sqrt{74}$.…(14分)
点评 本题考查了复数的运算法则、模的计算公式、几何意义,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<1} | B. | {x|-2≤x≤2} | C. | {x|1<x≤2} | D. | {x|x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
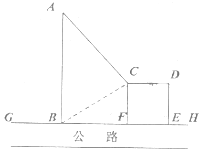 如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°..
如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°..查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com