
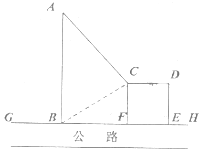
 如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°..
如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°..分析 (1)在△BCF中,CF=x,∠FBC=30°,CF⊥BF,BC=2x.在△ABC中,AB=y,AC=y-1,∠ABC=60°,由余弦定理,求解函数的解析式,然后求解定义域.
(2)求出M=30•(2y-1)+40x,通过基本不等式求解表达式的最值即可.
解答 (1)在△BCF中,CF=x,∠FBC=30°,CF⊥BF,所以BC=2x.
在△ABC中,AB=y,AC=y-1,∠ABC=60°,
由余弦定理,得AC2=BA2+BC2-2BA•BCcos∠ABC,…(2分)
即 ((y-1)2=y2+(2x)2-2y•2x•cos60°,
所以 $y=\frac{4{x}^{2}-1}{2x-2}$.…(5分)
由AB-AC<BC,得$2x>1,x>\frac{1}{2}$.又因为 $y=\frac{4{x}^{2}-1}{2x-2}$>0,所以x>1.
所以函数$y=\frac{4{x}^{2}-1}{2x-2}$的定义域是(1,+∞).…(6分)
(2)M=30•(2y-1)+40x.…(8分)
因为$y=\frac{4{x}^{2}-1}{2x-2}$.(x>1),所以M=30$•(2•\frac{4{x}^{2}-1}{2x-2}-1)+40x$
即 M=10$•(\frac{12{x}^{2}-3}{x-1}+4x-1)$.…(10分)
令t=x-1,则t>0.于是M(t)=10(16t+$\frac{9}{t}+25$),t>0,…(12分)
由基本不等式得M(t)≥10(2$\sqrt{144}+25$)=490,
当且仅当t=$\frac{3}{4}$,即x=$\frac{7}{4}$时取等号.…(15分)
答:当x=$\frac{7}{4}$km时,公司建中转站围墙和两条道路最低总造价M为490万元.…(16分)
点评 本题考查实际问题的应用,基本不等式求解表达式的最值,考查思想以及计算能力.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
 为了测量山顶M的海拔高度,飞机沿水平方向在A,B两点进行测量,A,B,M在同一个铅垂面内(如图).能够测量的数据有俯角、飞机的高度和A,B两点间的距离.请你设计一个方案,包括:
为了测量山顶M的海拔高度,飞机沿水平方向在A,B两点进行测量,A,B,M在同一个铅垂面内(如图).能够测量的数据有俯角、飞机的高度和A,B两点间的距离.请你设计一个方案,包括:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB⊥AC,AB=AC=2,AA1=3,M是侧棱CC1上一点.
如图,直三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB⊥AC,AB=AC=2,AA1=3,M是侧棱CC1上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com