已知圆(x+a)2+y2=1与圆x2+y2=16没有公共点.则正数a的取值范围为．题目和参考答案——青夏教育精英家教网—

1．已知圆（x+a）²+y²=1与圆x²+y²=16没有公共点，则正数a的取值范围为（0，3）∪（5，+∞）．

分析求解两个圆有公共点的范围，然后求解正数a的取值范围．

解答解：圆（x+a）²+y²=1圆心（-a，0）半径为1；圆x²+y²=16圆心（0，0）半径为4，
如果两个圆有公共点，可得3≤|a|≤5，解得a∈[3，5]∪[-5，-3]，
圆（x+a）²+y²=1与圆x²+y²=16没有公共点，则正数a的取值范围为：（0，3）∪（5，+∞）．
故答案为：（0，3）∪（5，+∞）．

点评本题考查圆与圆的位置关系的应用，逆向思维是解题的策略，考查计算能力．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

11．已知（$\root{3}{x}$+$\frac{1}{2\sqrt{x}}$）ⁿ（n∈N^*）的展开式中前三项的系数成等差数列．
（1）求展开式中二项式系数最大的项；
（2）求展开式中的有理项．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

12．平行四边形ABCD中，AB=2，AD=1，$∠BAD=\frac{π}{3}$，则|$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{AC}$|=2$\sqrt{7}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．

如图，某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树，已知角A为120°，AB，AC的长度均大于200米，现在边界AP，AQ处建围墙，在PQ处围竹篱笆．
（1）若围墙AP，AQ总长度为200米，如何围可使得三角形地块APQ的面积最大？
（2）已知AP段围墙高1米，AQ段围墙高1.5米，AP段围墙造价为每平方米150元，AQ段围墙造价为每平方米100元．若围围墙用了30000元，问如何围可使竹篱笆用料最省？

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

16．$cos（{-\frac{4π}{3}}）$=-$\frac{1}{2}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．

如图，在△ABC中，D是边BC上一点，$\overrightarrow{BD}=2\overrightarrow{DC}，|{\overrightarrow{AD}}$|=1．
（1）用$\overrightarrow{AB}，\overrightarrow{AD}$表示$\overrightarrow{AC}$；
（2）若$\overrightarrow{AB}•\overrightarrow{BD}+{\overrightarrow{AB}^2}$=0，求$\overrightarrow{AD}•\overrightarrow{AC}$的值；
（3）若AB=3，cos∠BAC=-$\frac{1}{3}$，求$|{\overrightarrow{BC}}$|．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

13．已知数列{a_n}满足a_n+2+a_n=a_n+1，且a₁=2，a₂=3，则a₂₀₁₇=2．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

10．已知集合M={x|x²＞4}，N={x|1＜x＜3}，则N∩（∁_RM）=（　　）

A．

{x|-2≤x＜1}

B．

{x|-2≤x≤2}

C．

{x|1＜x≤2}

D．

{x|x＜2}

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．

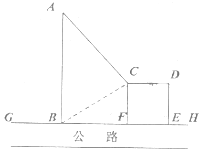如图，GH是东西方向的公路北侧的边缘线，某公司准备在GH上的一点B的正北方向的A处建设一仓库，设AB=ykm，并在公路北侧建造边长为xkm的正方形无顶中转站CDEF（其中EF在GH上），现从仓库A向GH和中转站分别修两条道路AB，AC，已知AB=AC+1，且∠ABC=60°．．
（1）求y关于x的函数解析式，并求出定义域；
（2）如果中转站四堵围墙造价为10万元/km，两条道路造价为30万元/km，问：x取何值时，该公司建设中转站围墙和两条道路总造价M最低．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学