
 为了测量山顶M的海拔高度,飞机沿水平方向在A,B两点进行测量,A,B,M在同一个铅垂面内(如图).能够测量的数据有俯角、飞机的高度和A,B两点间的距离.请你设计一个方案,包括:
为了测量山顶M的海拔高度,飞机沿水平方向在A,B两点进行测量,A,B,M在同一个铅垂面内(如图).能够测量的数据有俯角、飞机的高度和A,B两点间的距离.请你设计一个方案,包括:分析 (1)A,B点到M点的俯角α,β,飞机的高度h,A,B两点的距离a,画出图形.
(2)过点M作AB的垂线,垂足为N,第一步,在△ABM中,计算AM.第二步,在△AMN中,计算MN.第三步,计算山顶M海拔高度:h-MN
解答 解:(1)需测量的数据有:A,B点到M点的俯角α,β,飞机的高度h,A,B两点的距离a.…(4分)
(2)过点M作AB的垂线,垂足为N,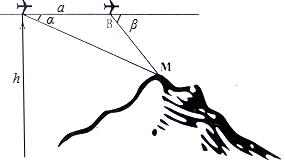
第一步,在△ABM中,计算AM.由正弦定理得$AM=\frac{{asin({π-β})}}{{sin({β-α})}}=\frac{asinβ}{{sin({β-α})}}$,…(8分)
第二步,在△AMN中,计算MN.由锐角三角函数定义得MN=AMsinα…(10分)
第三步,计算山顶M海拔高度:h-MN.…(12分)
点评 本题考查三角函数的实际应用,三角形的解法,数形结合以及计算能力.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<1} | B. | {x|-2≤x≤2} | C. | {x|1<x≤2} | D. | {x|x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
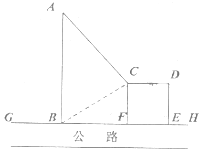 如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°..
如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°..查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com