
设A为椭圆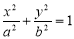 (
(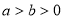 )上一点,点A关于原点的对称点为B,F为椭圆的右焦点,且AF⊥BF. 若∠ABF∈[
)上一点,点A关于原点的对称点为B,F为椭圆的右焦点,且AF⊥BF. 若∠ABF∈[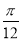 ,
,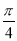 ],则该椭圆离心率的取值范围为 .
],则该椭圆离心率的取值范围为 .
【解析】
试题分析:设左焦点为F′,根据椭圆定义:|AF|+|AF′|=2a,根据B和A关于原点对称可知|BF|=|AF′|,推知|AF|+|BF|=2a,又根据O是Rt△ABF的斜边中点可知|AB|=2c,在Rt△ABF中用α和c分别表示出|AF|和|BF|代入|AF|+|BF|=2a中即可表示出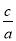 即离心率e,进而根据α的范围确定e的范围.
即离心率e,进而根据α的范围确定e的范围.
【解析】
∵B和A关于原点对称
∴B也在椭圆上
设左焦点为F′
根据椭圆定义:|AF|+|AF′|=2a
又∵|BF|=|AF′|∴|AF|+|BF|=2a …①
O是Rt△ABF的斜边中点,∴|AB|=2c
又|AF|=2csinα …②
|BF|=2ccosα …③
②③代入①2csinα+2ccosα=2a
∴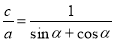
即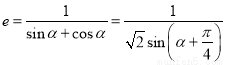
∵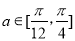 ,
,
∴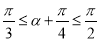
∴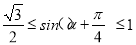
∴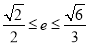
故答案为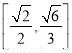
考点:椭圆的定义和性质.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源:2014-2015学年安徽省蚌埠市高一上学期期中考试数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数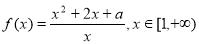 .
.
(1)当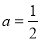 时,求函数
时,求函数 的最小值;
的最小值;
(2)若对任意的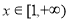 ,
, 恒成立,试求实数
恒成立,试求实数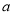 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省淮安市高三数学第一次调研测试理科数学试卷(解析版) 题型:解答题
在平面直角坐标系 中,已知曲线
中,已知曲线 的参数方程是
的参数方程是 (
(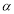 是参数),若以
是参数),若以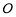 为极点,
为极点, 轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线
轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线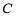 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省淮安市高三数学第一次调研测试理科数学试卷(解析版) 题型:填空题
若将甲、乙两个球随机放入编号为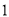 ,
,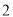 ,
,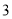 的三个盒子中,每个盒子的放球数量不限,则在
的三个盒子中,每个盒子的放球数量不限,则在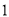 ,
,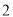 号盒子中各有一个球的概率是 .
号盒子中各有一个球的概率是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题12分)已知椭圆C的中心在坐标原点O,焦点在x轴上,离心率等于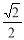 ,
,
它的一个顶点B恰好是抛物线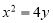 的焦点。
的焦点。
(1)求椭圆C的方程;
(2)直线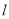 与椭圆C交于
与椭圆C交于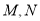 两点,那么椭圆C的右焦点
两点,那么椭圆C的右焦点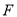 是否可以成为
是否可以成为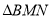 的垂心?若可以,求出直线
的垂心?若可以,求出直线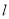 的方程;若不可以,请说明理由.(注: 垂心是三角形三条高线的交点)
的方程;若不可以,请说明理由.(注: 垂心是三角形三条高线的交点)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高二上学期期中考试理科数学试卷(解析版) 题型:选择题
设椭圆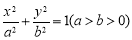 的离心率为
的离心率为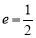 ,右焦点为F(c,0),方程
,右焦点为F(c,0),方程 的两个实根分别为x1和x2,则点P(x1,x2)的位置( )
的两个实根分别为x1和x2,则点P(x1,x2)的位置( )
A.必在圆 内
内
B.必在圆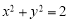 上
上
C.必在圆 外
外
D.以上三种情形都有可能
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高二上学期期中考试理科数学试卷(解析版) 题型:选择题
如图,一个几何体的三视图是由两个矩形和一个圆所组成,则该几何体的表面积是( )
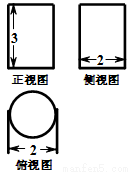
A.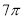 B.
B.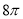 C.
C.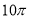 D.
D.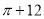
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习文科数学试卷(解析版) 题型:选择题
用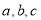 表示三条不同的直线,
表示三条不同的直线, 表示平面,给出下列命题:
表示平面,给出下列命题:
①若 ;
;
②若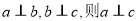 ;
;
③若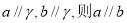 ;
;
④若 则
则 .
.
其中真命题的序号是( )
A.①② B.①④ C.②③ D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com