
分析 (1)设M(x,y),由kMA×kMB=-2,得$\frac{y}{x+1}•\frac{y}{x-1}=-2$,由此能求出点M的轨迹C的方程.
(2)由已知当直线PQ的斜率存在,设直线PQ的方程是y=kx+1,与椭圆联立,得(k2+2)x2+2kx-1=0,由此利用根的判别式、韦达定理、弦长公式,结合已知条件能求出△OPQ面积的最大值.
解答 解:(1)解:设M(x,y),(1分)
则${k}_{MA}=\frac{y}{x+1}$,${k}_{MB}=\frac{y}{x-1}$,x≠1,(3分)
∴$\frac{y}{x+1}•\frac{y}{x-1}=-2$,
∴点M的轨迹C的方程${x}^{2}+\frac{{y}^{2}}{2}=1$,x≠±1.(未写范围扣一分)(4分)
(2)由已知当直线PQ的斜率存在,设直线PQ的方程是y=kx+1,
联立$\left\{\begin{array}{l}{{x}^{2}+\frac{{y}^{2}}{2}=1}\\{y=kx+1}\end{array}\right.$,消去y得(k2+2)x2+2kx-1=0,
∵△=(4k2)+4(k2+2)=8(k2+1)>0,∴k∈R,
设P(x1,y1),Q(x2,y2),${x}_{1}+{x}_{2}=-\frac{2k}{{k}^{2}+2}$,${x}_{1}{x}_{2}=-\frac{1}{{k}^{2}+2}$,…(7分)
${S_{△OPQ}}=\frac{1}{2}×|{OF}|×|{{x_1}-{x_2}}|$
=$\frac{1}{2}\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}•{x_2}}=\sqrt{2}×\frac{{\sqrt{{k^2}+1}}}{{{k^2}+2}}$
=$\sqrt{2}×\frac{1}{{\sqrt{{k^2}+1}+\frac{1}{{\sqrt{{k^2}+1}}}}}≤\frac{{\sqrt{2}}}{2}$…(10分)
当且仅当k=0时取等号,…(11分)
△OPQ面积的最大值为$\frac{{\sqrt{2}}}{2}$.…(12分)
点评 本题考查点的轨迹方程的求法,考查三角形面积的最大值是否存在的判断与求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、弦长公式的合理运用.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
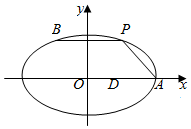 如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,且在x轴上方,$\overrightarrow{BP}$=$\overrightarrow{DA}$.
如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,且在x轴上方,$\overrightarrow{BP}$=$\overrightarrow{DA}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{{\sqrt{2}}}{2},1)$ | B. | $(\frac{{\sqrt{2}}}{2},1)$ | C. | $[\frac{{\sqrt{3}}}{2},1)$ | D. | $(\frac{{\sqrt{3}}}{2},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线PA1与PA2的斜率之和为定值$\frac{{a}^{2}}{{b}^{2}}$ | |
| B. | 直线PA1与PA2的斜率之积为定值$\frac{{a}^{2}}{{b}^{2}}$ | |
| C. | 直线PA1与PA2的斜率之和为定值$\frac{{b}^{2}}{{a}^{2}}$ | |
| D. | 直线PA1与PA2的斜率之积为定值$\frac{{b}^{2}}{{a}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com